Questõesde UERJ sobre Geometria Plana

InícioTodas as questões
1
1
1
Foram encontradas 44 questões
6ac815d9-e9
UERJ 2021 - Matemática - Áreas e Perímetros, Circunferências e Círculos, Geometria Plana

A figura a seguir representa uma circunferência de centro O e raio 1. Considere AC, BD e PQ diâmetros, com AC e BD perpendiculares. Observe-se ainda, que o ponto P pertence ao arco e o ponto R, ao raio OD; o segmento QR é paralelo a AC; e α é a medida do ângulo CÔP.

Sabendo que sen 2α = 2 senα . cosα, a área do triângulo PQR é igual a:

A

B

C
sen 2α
D
cos 2α
6acce5ee-e9
UERJ 2021 - Matemática - Áreas e Perímetros, Geometria Plana

Para confeccionar uma calha, foi utilizada uma chapa retangular de 0,6 m × 8 m. A chapa foi dobrada no formato de um paralelepípedo retângulo de altura x, comprimento igual a 8 m, e largura y, conforme as imagens a seguir.

Para que esse paralelepípedo tenha volume máximo, a altura x, em centímetros, deve ser igual a:

A
10
B
12
C
15
D
17
5eff17f4-fa
UERJ 2018 - Matemática - Aritmética e Problemas, Áreas e Perímetros, Razão, Proporção e Números Proporcionais, Geometria Plana

O Tangram é um quebra-cabeça chinês que contém sete peças: um quadrado, um paralelogramo e cinco triângulos retângulos isósceles. Na figura, o quadrado ABCD é formado com as peças de um Tangram.



Observe os seguintes componentes da figura:

• NP – lado do quadrado;

• AM – lado do paralelogramo;

• CDR e ADR – triângulos congruentes, bem como CNP e RST.


A razão entre a área do trapézio AMNP e a área do quadrado ABCD equivale a:

A
3/32
B
5/32
C
3/16
D
5/16
5ef0a122-fa
UERJ 2018 - Matemática - Progressão Aritmética - PA, Progressão Geométrica - PG, Geometria Plana, Triângulos, Progressões

Os triângulos A1B1C1, A2B2C2, A3B3C3, ilustrados abaixo, possuem perímetros p1, p2, p3, respectivamente. Os vértices desses triângulos, a partir do segundo, são os pontos médios dos lados do triângulo anterior.



Admita que

Assim, (p1, p2, p3) define a seguinte progressão:

A
aritmética de razão = – 8
B
aritmética de razão = – 6
C
geométrica de razão = 1/2
D
geométrica de razão = 1/4
f30c9457-b9
UERJ 2018 - Matemática - Aritmética e Problemas, Polígonos, Razão, Proporção e Números Proporcionais, Geometria Plana

O Tangram é um quebra-cabeça chinês que contém sete peças: um quadrado, um paralelogramo e cinco triângulos retângulos isósceles. Na figura, o quadrado ABCD é formado com as peças de um Tangram.


Observe os seguintes componentes da figura:
• NP – lado do quadrado;
• AM – lado do paralelogramo;
• CDR e ADR – triângulos congruentes, bem como CNP e RST.
A razão entre a área do trapézio AMNP e a área do quadrado ABCD equivale a:

A
3/32
B
5/32
C
3/16
D
5/16
f3000626-b9
UERJ 2018 - Matemática - Geometria Plana, Triângulos

Os triângulos A1B1C1, A2B2C2, A3B3C3, ilustrados abaixo, possuem perímetros p1, p2, p3, respectivamente. Os vértices desses triângulos, a partir do segundo, são os pontos médios dos lados do triângulo anterior.



Admita que
Assim, (p1, p2, p3) define a seguinte progressão:

A
aritmética de razão = – 8
B
aritmética de razão = – 6
C
geométrica de razão = 1/2
D
geométrica de razão = 1/4
f303e95c-b9
UERJ 2018 - Matemática - Circunferências e Círculos, Geometria Plana

O círculo a seguir tem o centro na origem do plano cartesiano xy e raio igual a 1. Nele, AP determina um arco de 120°.


As coordenadas de P são:

A
(-1/2, √3/2)
B
(-1/2, √2/2)
C
(-√3/2, 1/2)
D
(-√2/2, 1/2)
db42acb1-ba
UERJ 2011 - Matemática - Aritmética e Problemas, Áreas e Perímetros, Razão, Proporção e Números Proporcionais, Geometria Plana

As figuras a seguir mostram dois pacotes de café em pó que têm a forma de paralelepípedos retângulos semelhantes.


Se o volume do pacote maior é o dobro do volume do menor, a razão entre a medida da área total do maior pacote e a do menor é igual a:

A

B

C

D


c9911cc9-ba
UERJ 2011 - Matemática - Circunferências e Círculos, Geometria Plana

A figura abaixo representa um círculo de centro O e uma régua retangular, graduada em milímetros. Os pontos A, E e O pertencem à régua e os pontos B, C e D pertencem, simultaneamente, à régua e à circunferência.

O diâmetro do círculo é, em centímetros, igual a:

A
3,1
B
3,3
C
3,5
D
3,6
f1a664ae-bc
UERJ 2017 - Matemática - Quadriláteros, Geometria Plana, Triângulos

Considere na imagem abaixo:

• os quadrados ACFG e ABHI, cujas áreas medem, respectivamente, S1 e S2;
• o triângulo retângulo ABC;
• o trapézio retângulo BCDE, construído sobre a hipotenusa BC, que contém o ponto X.



Sabendo que CD = CX e BE = BX, a área do trapézio BCDE é igual a:

A
S1 + S2 / 2
B
S1 + S2 / 3
C
√S1 S2
D
√(S1)² + (S2)²
a2d57057-b9
UERJ 2015 - Matemática - Áreas e Perímetros, Geometria Plana

Na figura abaixo, estão representados dois círculos congruentes, de centros C1 e C2 , pertencentes ao mesmo plano α. O segmentomede 6 cm.


A área da região limitada pelos círculos, em cm² , possui valor aproximado de:

A
108
B
162
C
182
D
216
b9f89164-ba
UERJ 2015 - Matemática - Circunferências e Círculos, Geometria Plana

O raio de uma roda gigante de centro C mede = 10 m. Do centro C ao plano horizontal do chão, há uma distância de 11 m. Os pontos A e B, situados no mesmo plano vertical, ACB, pertencem à circunferência dessa roda e distam, respectivamente, 16 m e 3,95 m do plano do chão. Observe o esquema e a tabela:



θ (graus) sen θ
15º 0,259
30º 0,500
45º 0,707
60º 0,866

A medida, em graus, mais próxima do menor ângulo corresponde a:

A
45
B
60
C
75
D
105
7a22c779-ba
UERJ 2014 - Matemática - Áreas e Perímetros, Geometria Plana, Triângulos

Um triângulo equilátero possui perímetro P, em metros, e área A, em metros quadrados. Os valores de P e A variam de acordo com a medida do lado do triângulo.
Desconsiderando as unidades de medida, a expressão Y = P - A indica o valor da diferença entre os números P e A.

O maior valor de Y é igual a:

A
2√3
B
3√3
C
4√3
D
6√3
e90693c5-b9
UERJ 2013, UERJ 2013 - Matemática - Pontos e Retas, Relações Métricas no Triângulo Retângulo, Geometria Analítica, Geometria Plana

O gráfico abaixo mostra o segmento de reta AB, sobre o qual um ponto C (p, q) se desloca de A até B (3, 0).

O produto das distâncias do ponto C aos eixos coordenados é variável e tem valor máximo igual a 4,5.

O comprimento do segmento AB corresponde a:

A
5
B
6
C
3√5
D
6√2
e8fe7daf-b9
UERJ 2013, UERJ 2013 - Matemática - Aritmética e Problemas, Áreas e Perímetros, Razão, Proporção e Números Proporcionais, Geometria Plana

Na figura a seguir, estão representados o triângulo retângulo ABC e os retângulos semelhantes I, II e III, de alturas h1 , h2 e h3 respectivamente proporcionais às bases 

Se  = 4m e  = 3m, a razão 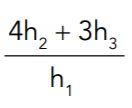 é igual a:

A
5
B
4
C
3
D
2
ed0d80ce-b9
UERJ 2016 - Matemática - Seno, Cosseno e Tangente, Circunferências e Círculos, Trigonometria, Polígonos, Geometria Plana

No esquema abaixo, estão representados um quadrado ABCD e um círculo de centro P e raio r,tangente às retas AB e BC. O lado do quadrado mede 3r.
A medida θ do ângulo CÂP pode ser determinada a partir da seguinte identidade trigonométrica:

                                                               tg (α - β) =  tg(α) - tg(β)/1 + tg(α) × tg(β) 


O valor da tangente de θ é igual a:

A
0,65
B
0,60
C
0,55
D
0,50
660affd3-b9
UERJ 2015, UERJ 2015 - Matemática - Áreas e Perímetros, Geometria Plana

Na figura abaixo, estão representados dois círculos congruentes, de centros C1 e C2 , pertencentes ao mesmo plano α. O segmento mede 6 cm.


A área da região limitada pelos círculos, em cm2 , possui valor aproximado de:

A
108
B
162
C
182
D
216
ac09dba6-f9
UERJ 2019 - Matemática - Polígonos, Geometria Plana

Três pentágonos regulares congruentes e quatro quadrados são unidos pelos lados conforme ilustra a figura a seguir.



Acrescentam-se outros pentágonos e quadrados, alternadamente adjacentes, até se completar o polígono regular ABCDEFGH...A, que possui dois eixos de simetria indicados pelas retas r e s. Se as retas perpendiculares r e s são mediatrizes dos lados AB e FG, o número de lados do polígono ABCDEFGH...A é igual a:

A
18
B
20
C
24
D
30