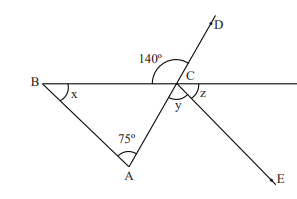
Na figura acima, CE é paralelo a
BA, a medida do ângulo 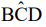 é igual a 140º e a medida do ângulo
é igual a 140º e a medida do ângulo 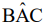 é 75º.
Então, os ângulos x, y e z medem, respectivamente,
é 75º.
Então, os ângulos x, y e z medem, respectivamente,

Na figura acima, CE é paralelo a
BA, a medida do ângulo 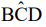 é igual a 140º e a medida do ângulo
é igual a 140º e a medida do ângulo 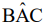 é 75º.
Então, os ângulos x, y e z medem, respectivamente,
é 75º.
Então, os ângulos x, y e z medem, respectivamente,
65º, 75º e 65º


 , então a razão
entre o volume e a área total desse cubo é
, então a razão
entre o volume e a área total desse cubo é


 = 1/2
= 1/2  . Se
. Se  = 12cm, as áreas
dos triângulos ABD e ADC, em cm
= 12cm, as áreas
dos triângulos ABD e ADC, em cm




