Questõessobre Geometria Plana
Na medicina, encontramos diversas aplicações da Matemática. Entre elas, a relação de Ehrenberg,
ln W = ln 2,4 + 0,0184h, que é uma fórmula que relaciona a altura h (em centímetros) com a massa W (em
quilogramas) de crianças de 5 a 13 anos. A massa aproximada ideal, em kg, de uma criança com 1,15 m é:
Um motociclista deseja saltar de uma rampa até outra, conforme a figura a seguir:

Ajustado o ângulo e a velocidade (m/s) do salto, ele modela a situação e chega à lei de formação
f(x) = -x² + 42x – 80. A distância horizontal deste salto foi de:
Um motociclista deseja saltar de uma rampa até outra, conforme a figura a seguir:

Ajustado o ângulo e a velocidade (m/s) do salto, ele modela a situação e chega à lei de formação
f(x) = -x² + 42x – 80. A distância horizontal deste salto foi de:
O número Phi (letra grega que se pronuncia "fi") tem este nome em homenagem ao arquiteto grego Phidias,
construtor do Parthenon, que utilizou esse número em muitas de suas obras. O número de ouro não é mais do que
um valor numérico resultado da divisão entre dois segmentos. Este número irracional é considerado, por muitos,
o símbolo da harmonia. Os egípcios também o utilizaram com as pirâmides. Por volta de 1500, com a vinda do
Renascentismo, Leonardo da Vinci colocou esta proporção natural em suas obras, por exemplo, no quadro Mona
Lisa. Na literatura, o número de ouro encontra sua aplicação mais notável no poema épico grego Ilíada, de
Homero. Quem o ler notará que a proporção entre as estrofes maiores e as menores dá um número próximo a  , o número de ouro, que também está presente nas sinfonias 5 e 9 de Ludwig van Beethoven. Os cartões
de crédito utilizam, na sua confecção, esta proporção.
, o número de ouro, que também está presente nas sinfonias 5 e 9 de Ludwig van Beethoven. Os cartões
de crédito utilizam, na sua confecção, esta proporção.

Sabendo que a medida do menor lado do cartão é 5,5cm, e mantendo a proporção de ouro, a medida do maior
lado do cartão é de aproximadamente:
 , o número de ouro, que também está presente nas sinfonias 5 e 9 de Ludwig van Beethoven. Os cartões
de crédito utilizam, na sua confecção, esta proporção.
, o número de ouro, que também está presente nas sinfonias 5 e 9 de Ludwig van Beethoven. Os cartões
de crédito utilizam, na sua confecção, esta proporção.
O artesanato indígena é de extrema beleza e de grande valor artístico, pois
representa a expressão cultural do povo indígena brasileiro. Já na época da
colonização do Brasil, os portugueses ficaram impressionados com a beleza
desse tipo de arte, que utiliza os elementos da natureza para a transformação em
objetos de enfeite ou utensílios domésticos. (Disponível em:
http:/www.suapesquisa.com). O cesto da figura (um cilindro equilátero de
diâmetro da base igual a 80 cm) é um exemplo do artesanato dos indígenas
brasileiros. A superfície total deste cesto, em m², é de:

Fonte: http://www.maisonsdumonde.com

Desde o início de uma obra (em sua demarcação inicial), até o acabamento final (durante a colocação dos pisos),
os pedreiros necessitam obter ângulos retos. O pedreiro, ao marcar 45 cm e 60 cm em duas laterais de paredes
que se interceptam e, depois, unir esses pontos para encontrar uma medida equivalente a 75 cm, utiliza, muitas
vezes mesmo sem ter conhecimento, um teorema matemático. O que, na linguagem dos pedreiros é chamado de
“deixar no esquadro”, equivale a uma aplicação do:
Considere a circunferência inscrita no triângulo
isósceles ABC, com 

A medida do segmento  em cm, é
em cm, é
Considere a circunferência inscrita no triângulo
isósceles ABC, com 

A medida do segmento  em cm, é
em cm, é


Uma lâmina deve ser confeccionada com a forma
apresentada na figura, em que  é paralelo a
é paralelo a 
 igual a 80º e
igual a 80º e  igual a 35º .
igual a 35º .

A medida do ângulo  , é
, é
Uma lâmina deve ser confeccionada com a forma
apresentada na figura, em que  é paralelo a
é paralelo a 
 igual a 80º e
igual a 80º e  igual a 35º .
igual a 35º .

A medida do ângulo  , é
, é
No triângulo retângulo ABC, a medida da bissetriz
interna é Sb = 5 cm e o ângulo a = 30°.

A medida do segmento  , em cm, é
, em cm, é
No triângulo retângulo ABC, a medida da bissetriz interna é Sb = 5 cm e o ângulo a = 30°.

A medida do segmento  , em cm, é
, em cm, é



Um veículo é projetado para percorrer trilhas que
necessitem de um sistema de tração com esteiras.
Uma parte da estrutura é mostrada na figura, com
os três círculos de raio = 10 cm.

Considerando que a esteira está completamente
esticada, seu comprimento, em cm, é





A área da região sombreada na figura, vale

A área da região sombreada na figura, vale






Na figura a seguir, o trapézio ABCD é retangular, e
AND é um triângulo de área igual a 112,5 m2
.
O valor de x, em metros, é




Considere o círculo inscrito no triângulo retângulo
da figura.

O perímetro do triângulo, em cm, é
Considere o círculo inscrito no triângulo retângulo da figura.

O perímetro do triângulo, em cm, é




Um marceneiro possui um pedaço de madeira no formato de
um triângulo retângulo, cujos catetos medem 12 cm e 35 cm. A
partir desta peça, ele precisa extrair o maior quadrado possível,
de tal forma que um dos ângulos retos do quadrado coincida
com o ângulo reto do triângulo. A medida do lado do quadrado
desejado pelo marceneiro está mais próxima de

Três triângulos equiláteros e dois quadrados formam uma
figura plana, como ilustrado. Seus centros são os vértices de um
pentágono irregular, que está destacado na figura. Se T é a área
de cada um dos triângulos e Q a área de cada um dos
quadrados, a área desse pentágono é

Três triângulos equiláteros e dois quadrados formam uma
figura plana, como ilustrado. Seus centros são os vértices de um
pentágono irregular, que está destacado na figura. Se T é a área
de cada um dos triângulos e Q a área de cada um dos
quadrados, a área desse pentágono é
Alice quer construir um paralelepípedo reto retângulo de
dimensões 60 cm x 24 cm x 18 cm, com a menor quantidade
possível de cubos idênticos cujas medidas das arestas são
números naturais. Quantos cubos serão necessários para
construir esse paralelepípedo?

Na figura, os segmentos AC e DE são paralelos entre si e
perpendiculares ao segmento CD; o ponto B pertence ao
segmento AC; F é o ponto médio do segmento AB; e ABE é um
triângulo equilátero. Além disso, o segmento BC mede 10
unidades de comprimento e o segmento AE mede 6 unidades
de comprimento. A medida do segmento DF, em unidades de
comprimento, é igual a

Na figura, os segmentos AC e DE são paralelos entre si e
perpendiculares ao segmento CD; o ponto B pertence ao
segmento AC; F é o ponto médio do segmento AB; e ABE é um
triângulo equilátero. Além disso, o segmento BC mede 10
unidades de comprimento e o segmento AE mede 6 unidades
de comprimento. A medida do segmento DF, em unidades de
comprimento, é igual a
Projetado pelo arquiteto Oscar Niemeyer, o Museu de Arte Contemporânea (MAC) tornou-se um dos cartões-postais da cidade de Niterói (Figura 1).

Considere que a forma da cúpula do MAC seja a de um tronco de cone circular reto (Figura 2), cujo diâmetro da base maior mede 50 m e 12 m é a distância entre as duas bases. A administração do museu deseja fazer uma reforma revitalizando o piso de seu pátio e, para isso, precisa estimar a sua área. (Utilize 1,7 como valor aproximado para √3 e 3 para π).

A medida da área do pátio do museu a ser revitalizada, em metro quadrado, está no intervalo


Dois atletas partem de pontos, respectivamente P1
e
P2
, em duas pistas planas distintas, conforme a figura,
deslocando-se no sentido anti-horário até a linha de
chegada, percorrendo, desta forma, a mesma distância
(L). Os trechos retos dos finais das curvas até a linha de
chegada desse percurso têm o mesmo comprimento (l)
nas duas pistas e são tangentes aos trechos curvos, que
são semicírculos de centro C. O raio do semicírculo maior
é R1
e o raio do semicírculo menor é R2
.

Sabe-se que o comprimento de um arco circular é
dado pelo produto do seu raio pelo ângulo, medido em
radiano, subentendido pelo arco.
Nas condições apresentadas, a razão da medida do
ângulo 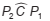 pela diferença L− l é dada por
pela diferença L− l é dada por

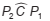 pela diferença L− l é dada por
pela diferença L− l é dada por Um vidraceiro precisa construir tampos de vidro com formatos diferentes, porém com medidas de áreas iguais.
Para isso, pede a um amigo que o ajude a determinar uma fórmula para o cálculo do raio R de um tampo de vidro
circular com área equivalente à de um tampo de vidro quadrado de lado L.

A fórmula correta é