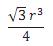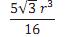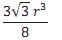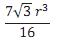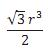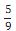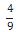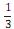Questões USP sobre Geometria Espacial

0d230b5c-99

USP 2019 - Matemática - Áreas e Perímetros, Geometria Plana, Geometria Espacial, Cilindro

O cilindro de papelão central de uma fita crepe tem raio externo de 3 cm. A fita tem espessura de 0,01 cm e dá 100 voltas completas. Considerando que, a cada volta, o raio externo do rolo é aumentado no valor da espessura da fita, o comprimento total da fita é de, aproximadamente,

Note e adote:

π ≡ 3,14.

A

9,4 m.

B

11,0 m.

C

18,8 m.

D

22,0 m.

E

25,1 m.

d11b1cf5-f2

USP 2018 - Matemática - Prismas, Geometria Espacial

A figura mostra uma escada maciça de quatro degraus, todos eles com formato de um paralelepípedo reto‐retângulo. A base de cada degrau é um retângulo de dimensões 20 cm por 50 cm, e a diferença de altura entre o piso e o primeiro degrau e entre os degraus consecutivos é de 10 cm. Se essa escada for prolongada para ter 20 degraus, mantendo o mesmo padrão, seu volume será igual a

A

2,1 m3

B

2,3 m3

C

3,0 m3

D

4,2 m3

E

6,0 m3

fbeba0bd-3b

USP 2014 - Matemática - Geometria Espacial, Cilindro

A grafite de um lápis tem quinze centímetros de comprimento e dois milímetros de espessura. Dentre os valores abaixo, o que mais se aproxima do número de átomos presentes nessa grafite é

Nota:
1) Assuma que a grafite é um cilindro circular reto, feito de grafita pura. A espessura da grafite é o diâmetro da base do cilindro.

2) Adote os valores aproximados de:
• 2,2 g/cm3 para a densidade da grafita;
• 12 g/mol para a massa molar do carbono;
• 6,0 x 1023 mol-1 para a constante de Avogadro.

A

5 x 1023

B

1 x 1023

C

5 x 1022

D

1 x 1022

E

5 x 1021

fbcbb316-3b

USP 2014 - Matemática - Geometria Espacial, Poliedros

O sólido da figura é formado pela pirâmide ܵSABCD sobre o paralelepípedo reto ABCDEFGH. Sabe-se que ܵS pertence à reta determinada por A e E e que AE = 2cm, AD = 4 cm e AB = 5 cm. A medida do segmento que faz com que o volume do sólido seja igual 4/3 do volume da pirâmide SEFGH é

A

2cm

B

4cm

C

6cm

D

8cm

E

10cm

f15f5be3-e4

USP 2012 - Matemática - Pirâmides, Áreas e Perímetros, Geometria Plana, Geometria Espacial

Os vértices de um tetraedro regular são também vértices de um cubo de aresta 2. A área de uma face desse tetraedro é

A

2

B

4

C

3

D

3

E

6

47cba03b-ab

USP 2013 - Matemática - Aritmética e Problemas, Razão, Proporção e Números Proporcionais, Prismas, Geometria Espacial, Poliedros

Três das arestas de um cubo, com um vértice em comum, são também arestas de um tetraedro. A razão entre o volume do tetraedro e o volume do cubo é;

A

1/8

B

1/6

C

2/9

D

1/4

E

1/3

95823eb7-12

USP 2011 - Matemática - Geometria Espacial, Poliedros

Em um tetraedro regular de lado a, a distância entre os pontos médios de duas arestas não adjacentes é igual a

A

B

C

D

E

6176f3d3-fc

USP 2010 - Matemática - Esfera, Geometria Espacial

A

B

C

D

E

6d40139e-fe

USP 2009 - Matemática - Pirâmides, Geometria Espacial

Uma pirâmide tem como base um quadrado de lado 1, e cada uma de suas faces laterais é um triângulo equilátero. Então, a área do quadrado, que tem como vértices os baricentros de cada uma das faces laterais, é igual a

A

B

C

D

E

Questõesde USP sobre Geometria Espacial

O sólido da figura é formado pela pirâmide ܵSABCD sobre o paralelepípedo reto ABCDEFGH. Sabe-se que ܵS pertence à reta determinada por A e E e que AE = 2cm, AD = 4 cm e AB = 5 cm. A medida do segmento que faz com que o volume do sólido seja igual 4/3 do volume da pirâmide SEFGH é

Os vértices de um tetraedro regular são também vértices de um cubo de aresta 2. A área de uma face desse tetraedro é

Três das arestas de um cubo, com um vértice em comum, são também arestas de um tetraedro. A razão entre o volume do tetraedro e o volume do cubo é;

Em um tetraedro regular de lado a, a distância entre os pontos médios de duas arestas não adjacentes é igual a

Uma pirâmide tem como base um quadrado de lado 1, e cada uma de suas faces laterais é um triângulo equilátero. Então, a área do quadrado, que tem como vértices os baricentros de cada uma das faces laterais, é igual a