3336da17-58
UNESP 2018 - Matemática - Análise de Tabelas e Gráficos, Funções, Equações Exponenciais
Observe, no plano cartesiano de eixos ortogonais, o gráfico
de duas funções exponenciais de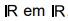

A intersecção desses gráficos ocorrerá em
Observe, no plano cartesiano de eixos ortogonais, o gráfico
de duas funções exponenciais de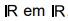

A intersecção desses gráficos ocorrerá em
A
infinitos pontos, localizados no 2° quadrante.
B
um único ponto, localizado no 2° quadrante.
C
um único ponto, localizado no 3° quadrante.
D
um único ponto, localizado no 1° quadrante.
E
um único ponto, localizado no 4° quadrante.

