Questõessobre Função de 1º Grau
Para P(x) = 7x + 7 e Q(x) = 23x + 9, se tivermos
4.900 plantas de capim, podemos ter 30 sapos
alimentando-se de insetos.
Q(x) representa a quantidade de consumidores
secundários da cadeia alimentar.
Uma locadora de filmes possui a seguinte regra para cobrança de multa para devoluções com atraso: para cada item locado, cobra R$ 2,50 para o primeiro dia de atraso e, a partir do segundo dia, R$ 0,50 a mais para cada dia de atraso. O cliente A está com uma grande quantidade de itens em atraso e, no décimo quinto dia, faz o seguinte acordo com a locadora: paga a metade da multa e, a cada 5 dias, pagará a metade do montante da multa; e o valor de R$ 0,50 por dia de atraso continuará sendo cobrado. Baseado nessas informações, assinale a alternativa correta.
Para cada m = 0,1,2,…, o termo 5m fornece o dia de
cada pagamento do cliente A, a partir do 15° dia de
atraso. A fórmula 19/2m+1 + 5/2(1 - 1/2m) fornece o valor em reais a ser pago para cada filme em atraso do
cliente A.
Uma locadora de filmes possui a seguinte regra para
cobrança de multa para devoluções com atraso: para cada
item locado, cobra R$ 2,50 para o primeiro dia de atraso
e, a partir do segundo dia, R$ 0,50 a mais para cada dia
de atraso. O cliente A está com uma grande quantidade
de itens em atraso e, no décimo quinto dia, faz o seguinte
acordo com a locadora: paga a metade da multa e, a cada
5 dias, pagará a metade do montante da multa; e o valor
de R$ 0,50 por dia de atraso continuará sendo cobrado.
Baseado nessas informações, assinale a alternativa correta.
Se n é o número de dias em atraso na entrega de um
filme, a fórmula M(n) = 0,5n - 2,5 fornece o valor
da multa a ser paga em reais.
A função g(x) = kx(P - x) é tal que g(x) = g(-x) para todo x real.
Assinale a alternativa correta.
Se P =100 e k = 0,01 , então (ƒ○ƒ)(x) possui
exatamente 3 raízes reais no intervalo 0 ≤ x ≤ 100.
Assinale a alternativa correta.
Devemos ter k ≤ 4/P para que a imagem de ƒ ainda
represente um valor possível para a população, para
todo 0 ≤ x ≤ P.
Assinale a alternativa correta.
O valor máximo de ƒ(x) é kP, para qualquer P.
Assinale a alternativa correta.
O conjunto imagem de ƒ está contido no
intervalo [0, +∞[.
FÍSICA - Formulário e Constantes
Um objeto é lançado do solo (origem) verticalmente para cima e retorna ao solo após k segundos. A altura que esse objeto se encontra do solo, em metros, em relação ao tempo t, em segundos, é dada pela função ƒ :[0,k] → ℝ definida por ƒ(t) = 40t − 5t2 em que ƒ(0) corresponde à sua altura no instante do lançamento. A esse respeito, considerando seus conhecimentos sobre Funções e sobre Cinemática e desprezando a resistência do ar, assinale o que for correto.
A altura máxima alcançada pelo objeto é 100 m.
FÍSICA - Formulário e Constantes
Um objeto é lançado do solo (origem) verticalmente para cima e retorna ao solo após k segundos. A altura que esse objeto se encontra do solo, em metros, em relação ao tempo t, em segundos, é dada pela função ƒ :[0,k] → ℝ definida por ƒ(t) = 40t − 5t2 em que ƒ(0) corresponde à sua altura no instante do lançamento. A esse respeito, considerando seus conhecimentos sobre Funções e sobre Cinemática e desprezando a resistência do ar, assinale o que for correto.
A função ƒ é injetora.
FÍSICA - Formulário e Constantes
Um objeto é lançado do solo (origem) verticalmente para cima e retorna ao solo após k segundos. A altura que esse objeto se encontra do solo, em metros, em relação ao tempo t, em segundos, é dada pela função ƒ :[0,k] → ℝ definida por ƒ(t) = 40t − 5t2 em que ƒ(0) corresponde à sua altura no instante do lançamento. A esse respeito, considerando seus conhecimentos sobre Funções e sobre Cinemática e desprezando a resistência do ar, assinale o que for correto.
Pela taxa de variação da função y,
seu gráfico
é uma reta crescente.
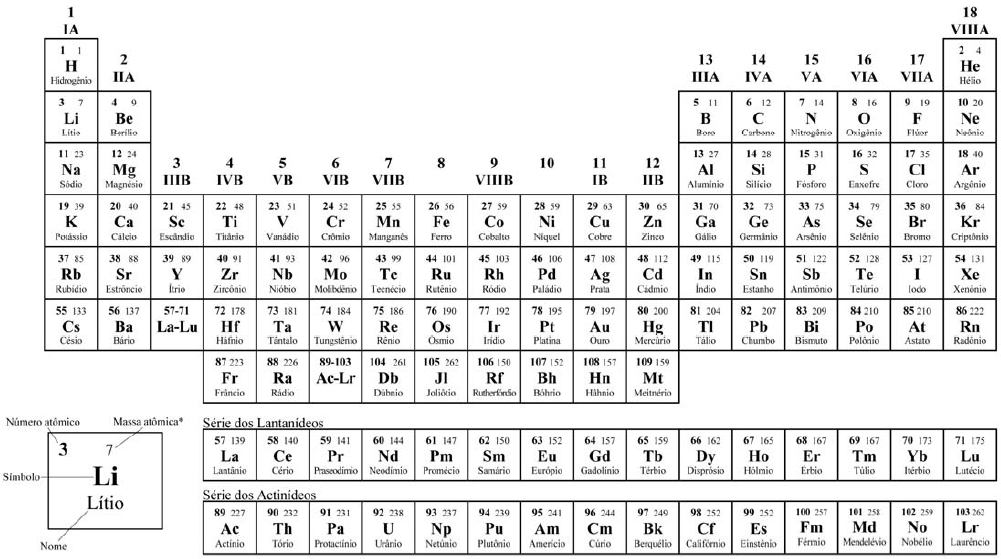
*OS VALORES DAS MASSAS ATÔMICAS DOS ELEMENTOS FORAM ARREDONDADOS PARA FACILITAR OS CÁLCULOS. ESTA TABELA PERIÓDICA É EXCLUSIVA PARA ESTE VESTIBULAR E NÃO DEVE SER UTILIZADA PARA OUTRAS FINALIDADES.
Cx Hy é a fórmula geral para um determinado grupo de compostos químicos, muitos deles utilizados como combustíveis na indústria e em automóveis. Sabendo-se que y = 2x + 2 , assinale o que for correto. (Dados: C = 12,0 u; H = 1,0 u).
O gráfico da função y é uma parábola.

*OS VALORES DAS MASSAS ATÔMICAS DOS ELEMENTOS FORAM ARREDONDADOS PARA FACILITAR OS CÁLCULOS. ESTA TABELA PERIÓDICA É EXCLUSIVA PARA ESTE VESTIBULAR E NÃO DEVE SER UTILIZADA PARA OUTRAS FINALIDADES.
Cx Hy é a fórmula geral para um determinado grupo de compostos químicos, muitos deles utilizados como combustíveis na indústria e em automóveis. Sabendo-se que y = 2x + 2 , assinale o que for correto. (Dados: C = 12,0 u; H = 1,0 u).
A função ƒ : A → B é injetora.
A função ƒ : A → B é sobrejetora.
Se a Tiamina pertencesse ao conjunto A, para
que ƒ continuasse a ser uma função,
deveríamos incluir no conjunto B, as
vitaminas.
É possível incluir mais elementos no conjunto
A de modo que ƒ seja uma função bijetora.
A utilização de uma escala logarítmica facilita a
visualização do aumento drástico da incidência
de câncer, com o aumento da idade.

No eixo vertical do gráfico, existe um ponto
indicado por “ • ”, sem legenda. Nesse ponto,
deveria haver uma legenda indicando um
número entre 600 e 700.
