Questõesde UFPR sobre Funções

InícioTodas as questões
1
1
1
Foram encontradas 10 questões
a0ab82d4-67
UFPR 2021 - Matemática - Funções, Equações Exponenciais

O estágio inicial de um modelo epidemiológico, que mede o número de pessoas infectadas em uma população, é descrito pela função I(t) = I02rt ,em que I(t) representa o número de infectados da população,  I0 > 0 representa o número inicial de infectados,  r > representa a taxa de contágio e t é o tempo medido em dias desde o início da epidemia. Com relação ao número de infectados, é correto afirmar: 

A
Caso a taxa de infectados r esteja no intervalo (0,1), então o número de infectados I(t) decresce conforme os dias passam.
B
Caso I0  = 3 e r = 2,3, então o número de infectados I(t) aumenta desde o primeiro dia até atingir um máximo por volta do sexto dia, e depois começa a decrescer.  
C
Caso I0  = 1 e r = 1, então a cada dia que passa a quantidade de infectados  I(t) aumenta em 2.
D
Caso I0  = 1 e r = 0,5, então é necessário pelo menos 20 dias para que o número de infectados  I(t)  seja maior que 1.000
E
Se a taxa de contágio r aumentar, então haverá menos pessoas infectadas conforme os dias passam.
5927b883-bf
UFPR 2019 - Matemática - Funções, Função de 1º Grau

Define-se o erro da função f para o ponto (x,y) como sendo o valor \ f(x) —y\ e o erro de f para o conjunto de pontos C como sendo a soma dos erros de f para todos os pontos de C. Entre as funções abaixo, qual possui o menor erro para o conjunto C = {(0,5), (1,3), (2, —1)}?

A
fa(x) = —2,5x + 5.
B
fb(x) = —4x + 7.
C
fc(x) = —3x + 6
D
fd(x) = —3,5x + 5
E
fe(x) = —4x + 6.
36b3accf-b0
UFPR 2011, UFPR 2011, UFPR 2011, UFPR 2011, UFPR 2011 - Matemática - Funções, Logaritmos

Para se calcular a intensidade luminosa L, medida em lumens, a uma profundidade de x centímetros num determinado lago, utiliza-se a lei de Beer-Lambert, dada pela seguinte fórmula:


log (L /15 ) = −0,08x


Qual a intensidade luminosa L a uma profundidade de 12,5 cm?

A
150 lumens.
B
15 lumens.
C
10 lumens.
D
1,5 lumens.
E
1 lúmen.
ab6bed16-dd
UFPR 2018 - Matemática - Funções, Equações Exponenciais

Um tanque contém uma solução de água e sal cuja concentração está diminuindo devido à adição de mais água. Suponha que a concentração Q(t) de sal no tanque, em gramas por litro (g/l), decorridas t horas após o início da diluição, seja dada por


                                Q(t) = 100 x 5 -0,3t


Assinale a alternativa que mais se aproxima do tempo necessário para que a concentração de sal diminua para 50 g/l.

(Use log5 = 0,7)

A
4 horas e 45 minutos.
B
3 horas e 20 minutos.
C
2 horas e 20 minutos.
D
1 hora e 25 minutos.
E
20 minutos.
cfbe8fb4-be
UFPR 2017 - Matemática - Funções, Função de 2º Grau

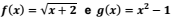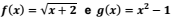Sobre as funções reais , identifique as afirmativas a seguir como verdadeiras (V) ou falsas (F):


( ) O domínio da função ƒ é Dom(ƒ) = {x ∈ ℝ; x ≥ 0}.

( )

( ) A imagem de ƒ coincide com a imagem de g, ou seja, Im(ƒ) = Im(g).

( ) Os gráficos dessas funções se cruzam apenas uma vez.


Assinale a alternativa que apresenta a sequência correta, de cima para baixo.

A
F – V – F – F.
B
V – V – F – V.
C
V – F – V – F.
D
F – V – V – F.
E
V – F – F – V.
cfaa95dc-be
UFPR 2017 - Matemática - Funções, Função de 1º Grau

A figura ao lado representa o quadrilátero do plano cartesiano delimitado pelo eixo das abscissas e pelo gráfico das seguintes funções:


ƒ(x) = 2x + 4, se -2 ≤ x ≤ 1;

g(x) = 1/9(2x + 52), se 1 ≤ x ≤ 10;

h(x) = 2(14 - x), se 10 ≤ x ≤ 14;


Qual é a área desse quadrilátero?

A

75.

B
88.
C
95.
D
100.
E
128.
3546d1eb-3b
UFPR 2016 - Matemática - Funções, Equações Exponenciais

Suponha que a quantidade Q de um determinado medicamente no organismo t horas após sua administração possa ser calculada pela fómula:

Q = 15 . (1/10)2t


sendo Q medindo em miligramas. A expressão que fornece o tempo t em função da quantidade de medicamento Q é:

A
t = log√15/Q
B
t = log15/2logQ
C
t = 10√log(Q/15)
D
t =1/2 log Q/15
E
t = log Q2/225
3543fc3c-3b
UFPR 2016 - Matemática - Funções, Função de 1º Grau, Função de 2º Grau

A respeito da função representada no gráfico ao lado, considere as seguintes afirmativas: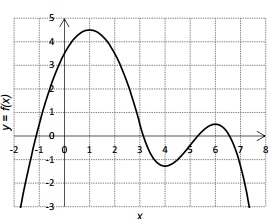


1. A função é crescente no intervalo aberto (4, 6).
2. A função tem um ponto de máximo em x = 1.
3. Esse gráfico representa uma função injetora.
4. Esse gráfico representa uma função polinomial de terceiro grau.

Assinale a alternativa correta.

A
Somente as afirmativas 1 e 2 são verdadeiras.
B
Somente as afirmativas 1 e 3 são verdadeiras.
C
Somente as afirmativas 3 e 4 são verdadeiras.
D
Somente as afirmativas 1, 2 e 4 são verdadeiras.
E
Somente as afirmativas 2, 3 e 4 são verdadeiras.
bfb995e5-b3
UFPR 2015 - Matemática - Funções, Equação Logarítmica

Considere o gráfico da função f(x) = log2x e a reta r que passa pelos pontos A e B, como indicado na figura ao lado, sendo k a abscissa do ponto em que a reta r intersecta o eixo Ox. Qual é o valor de k?


A
17/12.
B
14/11.
C
12/7.
D
11/9.
E
7/4.
bfbe45d3-b3
UFPR 2015 - Matemática - Funções, Equações Exponenciais

A análise de uma aplicação financeira ao longo do tempo mostrou que a expressão V(t) = 1000.20,0625.t fornece uma boa aproximação do valor V (em reais) em função do tempo t (em anos), desde o início da aplicação. Depois de quantos anos o valor inicialmente investido dobrará?

A
8.
B
12.
C
16.
D
24.
E
32.