Considere o caso abaixo e analise as afirmações a seguir.
Nos seres humanos a falta de vitamina D é associada ao risco de câncer, obesidade e uma série de
outras doenças. Em certas épocas do ano, em determinada localidade, percebeu-se o aumento de
casos de doenças associadas à falta de vitamina D.
Nesse sentido, um estudo realizado modelou o número de horas com luz solar L (t) dessa localidade,
em função do dia t do ano, através da função:

Dessa forma, 1° de janeiro corresponde a t =1,
o dia 2 de janeiro é indicado por t = 2 , e assim
sucessivamente, até que 31 de julho corresponde a
t = 212.
I Com base na função L(t), o dia que possui o maior número de horas com luz solar nessa localidade ocorre no mês de fevereiro.
II A função L(t) indica que o número mínimo de horas com luz solar nessa localidade, para algum dia do intervalo dado, é igual a 9,2 horas.
III O dia que possui o maior número de horas com luz solar nessa localidade ocorre para t =159.
IV O período da função L(t) é 2π .
Todas as afirmações corretas estão em:
Considere o caso abaixo e analise as afirmações a seguir.
Nos seres humanos a falta de vitamina D é associada ao risco de câncer, obesidade e uma série de outras doenças. Em certas épocas do ano, em determinada localidade, percebeu-se o aumento de casos de doenças associadas à falta de vitamina D. Nesse sentido, um estudo realizado modelou o número de horas com luz solar L (t) dessa localidade, em função do dia t do ano, através da função:

Dessa forma, 1° de janeiro corresponde a t =1, o dia 2 de janeiro é indicado por t = 2 , e assim sucessivamente, até que 31 de julho corresponde a t = 212.
I Com base na função L(t), o dia que possui o maior número de horas com luz solar nessa localidade ocorre no mês de fevereiro.
II A função L(t) indica que o número mínimo de horas com luz solar nessa localidade, para algum dia do intervalo dado, é igual a 9,2 horas.
III O dia que possui o maior número de horas com luz solar nessa localidade ocorre para t =159.
IV O período da função L(t) é 2π .
Todas as afirmações corretas estão em:
I - II - III

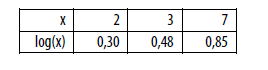

 ?
?
 = 3 com x, y, z
= 3 com x, y, z