Questõessobre Funções Trigonométricas e Funções Trigonométricas Inversas

InícioTodas as questões
1
1
Foram encontradas 134 questões
f04c4531-f9
IF-PR 2019 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Em uma determinada região litorânea, a maré oscila segundo a função h(t) = 3 – 2sen( πt/ 12 ), sendo h a altura em metros, que a maré atinge no tempo t em horas, medido a partir de 6h da manhã. Uma embarcação, que se encontra encalhada às 11h da manhã, precisa de uma profundidade mínima de 2 metros para navegar. Assinale a alternativa que apresenta quantas horas os tripulantes dessa embarcação ainda terão que esperar para prosseguirem viagem.

A
4h.
B
5h.
C
6h.
D
7h.
077b8369-ba
UNEB 2016 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Admitindo-se que o peso de determinada pessoa, ao longo de uma ano, possa ser modelado pela função P(t) = 65 − 5cos , em que t =1,...,12 corresponde aos meses de janeiro a dezembro e considerando √3 = 1,7, pode-se estimar que, de maio até agosto, o peso dessa pessoa

A
diminuiu 4,50kg.
B
aumentou 4,50kg.
C
diminuiu 6,75kg.
D
aumentou 6,75kg
E
diminuiu 7,56kg.
db00fec9-e0
FAG 2016 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

O conjunto-imagem da função f definida por f(x) = sen (x) + h é [ -2; 0 ]. O valor de h é

A
π
B
-2
C
-1
D
0
E
1
33a143c8-f1
Univap 2016 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

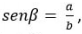Sabendo que com 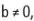um possível valor para 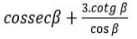é

A
4b/a
B
a/b
C
2a/b
D
b/a
E
a/4b
2a084364-e0
FAG 2016 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

O conjunto-imagem da função f definida por f(x) = sen (x) + h é [ -2; 0 ]. O valor de h é

A
π
B
-2
C
-1
D
0
E
1
a61416e2-b2
UPE 2016 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Se a função trigonométrica y = a + bsen(px) tem imagem l = [1, 5] e período 3/π , qual é o valor da soma a + b + p? Adote π=3

A
5
B
6
C
8
D
10
E
11
e9a3e29f-b3
IF-MT 2016 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Considerando-se a expressão trigonométrica x= 1+ cos45°, um dos possíveis produtos que a representam é igual a:

A
2cos222° 30'
B
4cos222°30'
C
2cos2 45°
D
3-2sen2 22°30'
E
3+2sen2 22°30'
abd53b70-b3
IF-PR 2016 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Sendo x e a, números reais tais que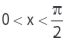 e sec x = a – 1, então tg2 x é igual a:

A
a(a – 2).
B
a(a – 1).
C
a2.
D
1 – a2 .
7d8c0ad8-b6
UFVJM-MG 2017 - Matemática - Análise de Tabelas e Gráficos, Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

O gráfico a seguir mostra como foi o consumo de energia de uma casa ao longo dos 12 meses de um determinado ano.


Através das informações contidas no gráfico conseguiu-se uma função definida por mais de uma sentença que relaciona o consumo y em função do tempo x em meses, onde a e b são constantes.


Analisando a função e seu gráfico, podemos afirmar que o valor de a + b é:

A
2
B
3
C
4
D
5
cf18ca93-b5
FEI 2014 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

O conjunto solução de | 2cosx | <1, para 0 ≤ x < 2π, é:

A

B

C

D

E

82800f19-b8
UECE 2013 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Se p e q são duas soluções da equação 2sen²x – 3sen x + 1 = 0 tais que senp ≠ senq, então o valor da expressão sen²p – cos²q é igual a

A
0.
B
0,25.
C
0,50.
D
1.
82640a92-b8
UECE 2013 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Se f: R→R é a função definida por f(x) = 2senx +1, então o produto do maior valor pelo menor valor que f assume é igual a

A
4,5.
B
3,0.
C
1,5.
D
0.
dfdd78ef-f4
UEG 2019 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Resolvendo-se a equação sen 2x = 1, encontramos a 1ª determinação positiva de x igual a

A
π/2
B
π/3
C
π/4
D
π/6
E
π/12
f73c1511-e2
UEPB 2011 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Sendo f uma função definida por , f(x) = sen (x/2), 0 ≤ x ≤ 4π , então f (x) é positiva, quando:

A
0 < x < 2π
B
0 < x < 4π
C
–π ≤ x ≤ 2π
D
–π < x < π
E
0 < x < 6π
f584d6ac-d9
FAMERP 2019 - Matemática - Pontos e Retas, Trigonometria, Geometria Analítica, Funções Trigonométricas e Funções Trigonométricas Inversas

A figura indica os gráficos de uma reta r e uma senoide s, de equações e y = 5/2 e y = 1 + 3 sen (2x), em um plano cartesiano de eixos ortogonais.




Sendo P um ponto de intersecção dos gráficos, conforme mostra a figura, sua abscissa, convertida para graus, é igual a

A
275º
B
240º
C
225º
D
210º
E
195º
e3f46bfd-de
Unimontes - MG 2019 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Se f0 [0,4 π ] ⟶ ℜ é uma função definida por f(x) = sen x - cos x , então a equação f(x)= 0 tem

A
somente uma raiz real.
B
duas raízes reais.
C
três raízes reais
D
quatro raízes reais.
0e1aeb7c-ef
Inatel 2019 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

O valor máximo assumido pela função f (x) = - 3 - 4 cos (5x) é dado por:

A
-7
B
-4
C
-3
D
1
E
5
c804ac5c-e8
UEFS 2011 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas



As telhas onduladas de amianto, bastante populares, vêm tendo seu uso proibido em diversos municípios brasileiros, por ser um material cancerígeno e por também poder causar doenças respiratórias. Para substituí-las, podem ser usadas as chamadas ecotelhas — telhas onduladas produzidas a partir da reciclagem de material plástico, como, por exemplo, aparas de tubos de creme dental.

As ecotelhas têm elevada resistência mecânica, bem como à ação dos raios ultravioleta e infravermelho, além de serem econômicas, são 100% impermeáveis. Supondo-se que a curva representativa de uma secção transversal de uma telha ondulada, como a da figura, seja definida por parte da função real f(x) = 1 − 2sen ( x/2- 5π/3), é correto afirmar que o conjunto-imagem e o período de f(x) são, respectivamente,

A
[−1, 3] e 4π.
B
[−3, 1] e 4π.
C
[−1, 3] e 3π.
D
[−1, 1] e 2π.
E
[−3, 3] e 2π.
0c988ee6-e7
UEFS 2009 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

O conjunto-imagem da função real f(x) = | – 3 + cos (2x)| + 1 é

A
[1, 2]
B
[2, 3]
C
[2, 4]
D
[3, 4]
E
[3, 5]
e5afe6f3-e7
UEFS 2010 - Matemática - Circunferências e Círculos, Trigonometria, Geometria Plana, Funções Trigonométricas e Funções Trigonométricas Inversas

Em um parque de diversões, uma roda gigante de raio r = 10m, tendo 12 cadeiras igualmente espaçadas ao longo de seu perímetro, faz uma volta completa em 30 segundos. Além disso, o ponto mais baixo atingido ao longo do percurso circular está a 0,5m do solo. Certo dia, depois de todos os assentos estarem ocupados, o assento 1 se encontrava na posição indicada na figura, quando a roda começa a girar no sentido anti-horário.



Sendo a distância desse assento ao solo, t segundos após a roda ter começado a girar, dada pela expressão D(t) =M+N sen(αt), α > 0, é correto afirmar que M − N é igual a

A
cos(5α)
B
sen(5α)
C
cos(10α)
D
sen(10α)
E
cos(15α)