TEXTO 5
É com certa sabedoria que se diz: pelos olhos
se conhece uma pessoa. Bem, há olhares de todos os
tipos — dos dissimulados aos da cobiça, seja pelo vil
metal ou pelo sexo.
Garimpeiro se conhece pelos olhos. Olhos de
febre, que flamejam e reluzem. Há, em suas pupilas,
o ouro. O brilho dourado tatua a íris. Trata-se apenas
de um reflexo de sua alma e daquilo que corre em
suas veias. É um vírus. A princípio, um sonho distante,
mas, ao correr dos dias, torna-se uma angustiante
busca. Na primeira vez que o ouro fagulha na sua
frente, na bateia, toda a alma se contamina e o vírus
se transforma em doença incurável.
Todos, no garimpo, têm histórias semelhantes.
Têm família, filhos, empregos em suas
cidades, nos distantes estados, mas, de repente,
espalha-se a notícia do ouro. Então, largam tudo,
vendem a roupa do corpo e lá se vão. Caçar o rastro
do ouro é a sina. Nos olhos, a febre — um brilho
dourado doentio. Sim, é fácil conhecer um garimpeiro.
Todos sabem que, no garimpo, não é lugar
para se viver. Mas ninguém abandona o seu posto.
Suor, lama, pedregulhos, pepitas douradas, cansaço
— é a vida que até o diabo rejeita.
Por onde passam, o rastro da destruição. A Amazônia é nossa. Tratores e retroescavadeiras derrubam
e limpam a floresta; as dragas chegam, os
rios se contaminam rapidamente de mercúrio. Quem
pode mais chora menos. Na trilha do brilho dourado,
nada se preserva. Ai daqueles que levantarem alguma
voz... No dia seguinte, o corpo é encontrado no meio
da selva, um bom prato aos bichos.
(GONÇALVES, David. Sangue verde. Joinville: Sucesso
Pocket, 2014. p. 5-6. Adaptado.)
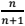 , onde
, onde 



