Questõessobre Estudo da Reta
No plano cartesiano, os pontos (x,y) que satisfazem a equação x² - 5x + 4 = 0 são representados por
uma parábola com abscissa do vértice igual a -5/2
A figura representa o globo terrestre e nela estão
marcados os pontos A, B e C. Os pontos A e B estão
localizados sobre um mesmo paralelo, e os pontos B e
C, sobre um mesmo meridiano. É traçado um caminho do
ponto A até C, pela superfície do globo, passando por B,
de forma que o trecho de A até B se dê sobre o paralelo
que passa por A e B e, o trecho de B até C se dê sobre o
meridiano que passa por B e C. Considere que o plano a
é paralelo à linha do equador na figura.

A projeção ortogonal, no plano α, do caminho traçado no
globo pode ser representada por
A figura representa o globo terrestre e nela estão marcados os pontos A, B e C. Os pontos A e B estão localizados sobre um mesmo paralelo, e os pontos B e C, sobre um mesmo meridiano. É traçado um caminho do ponto A até C, pela superfície do globo, passando por B, de forma que o trecho de A até B se dê sobre o paralelo que passa por A e B e, o trecho de B até C se dê sobre o meridiano que passa por B e C. Considere que o plano a é paralelo à linha do equador na figura.

A projeção ortogonal, no plano α, do caminho traçado no globo pode ser representada por





O objetivo da Geometria Analítica (GA) é estudar entes
geométricos, como retas e circunferências, por meio de métodos
algébricos que envolvem equações e fórmulas. Por exemplo, a
GA estuda uma reta por meio de sua equação, que é uma
igualdade do tipo ax + by + c = 0, com a, b e c sendo números
reais.
Dadas as afirmativas acerca do estudo analítico de retas.
I. As retas 2x + y – 3 = 0 e 4x + 2y – 1 = 0 são paralelas.
II. As retas x + 3y = 0 e 3x – y = 0 são perpendiculares.
III. A reta 2x – y + 4 = 0 não contém a origem dos eixos
cartesianos.
Verifica-se que está(ão) correta(s)
O objetivo da Geometria Analítica (GA) é estudar entes geométricos, como retas e circunferências, por meio de métodos algébricos que envolvem equações e fórmulas. Por exemplo, a GA estuda uma reta por meio de sua equação, que é uma igualdade do tipo ax + by + c = 0, com a, b e c sendo números reais.
Dadas as afirmativas acerca do estudo analítico de retas.
I. As retas 2x + y – 3 = 0 e 4x + 2y – 1 = 0 são paralelas.
II. As retas x + 3y = 0 e 3x – y = 0 são perpendiculares.
III. A reta 2x – y + 4 = 0 não contém a origem dos eixos cartesianos.
Verifica-se que está(ão) correta(s)
Dois amigos caminham no plano xy, ao longo de
retas paralelas cujas equações são 2x + 5y = 7 e
3x + my = 1. Então, o valor de m é
Devido ao aumento do fluxo de passageiros, uma
empresa de transporte coletivo urbano está fazendo
estudos para a implantação de um novo ponto de parada
em uma determinada rota. A figura mostra o percurso,
indicado pelas setas, realizado por um ônibus nessa rota
e a localização de dois de seus atuais pontos de parada,
representados por P e Q.
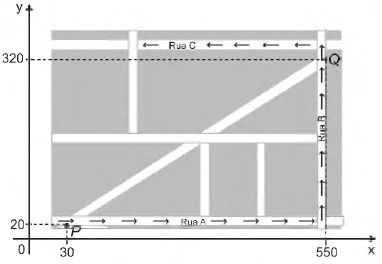
Os estudos indicam que o novo ponto T deverá
ser instalado, nesse percurso, entre as paradas
já existentes P e Q, de modo que as distâncias
percorridas pelo ônibus entre os pontos P e T e entre
os pontos T e Q sejam iguais.
De acordo com os dados, as coordenadas do novo ponto
de parada são

Os estudos indicam que o novo ponto T deverá ser instalado, nesse percurso, entre as paradas já existentes P e Q, de modo que as distâncias percorridas pelo ônibus entre os pontos P e T e entre os pontos T e Q sejam iguais.
De acordo com os dados, as coordenadas do novo ponto de parada são
Determine a equação da reta que passa pela origem
do sistema cartesiano e é tangente à parábola de
equação x2 − y + 2 = 0 num ponto do 2º quadrante.
x + √2 y = 0
4
Observe as coordenadas cartesianas de cinco pontos:
A(0,100), B(0, -100), C(10, 100), D(10, -100), E(100, 0).
Se a reta de equação reduzida y = mx + n é tal que mn > 0, então, dos cinco pontos dados anteriormente, o único que certamente não pertence ao gráfico dessa reta é
A(0,100), B(0, -100), C(10, 100), D(10, -100), E(100, 0).
Se a reta de equação reduzida y = mx + n é tal que mn > 0, então, dos cinco pontos dados anteriormente, o único que certamente não pertence ao gráfico dessa reta é
O retângulo ABCD tem um lado sobre o eixo x e um lado
sobre o eixo y como mostra a figura. A área do retângulo
ABCD é 15 e a medida do lado AB é 5. A equação da reta
que passa por D e por B é:

O retângulo ABCD tem um lado sobre o eixo x e um lado sobre o eixo y como mostra a figura. A área do retângulo ABCD é 15 e a medida do lado AB é 5. A equação da reta que passa por D e por B é:

O coeficiente angular da reta tangente à curva x3 + sen y + xy3 – 1 = 0, no ponto (1, 0), é igual a –3.
Considerando-se, no espaço R3 , os pontos A = (1, 2, 1), B = (2, 0, 2), C = (4, k, 4) e o plano α de equação x – 2y + 2z + 4 = 0, é correto afirmar:
A reta definida por  é paralela ao vetor
é paralela ao vetor  .
.
Considerando-se, no espaço R3 , os pontos A = (1, 2, 1), B = (2, 0, 2), C = (4, k, 4) e o plano α de equação x – 2y + 2z + 4 = 0, é correto afirmar:
A reta definida por  é paralela ao vetor
é paralela ao vetor  .
.
Dados os pontos A(1,7), B(− 2, 1), C(2, 5) e D(− 1, − 4), e sabendo que  indica o coeficiente angular da reta que passa pelos pontos A e B, considere as seguintes afirmações:
indica o coeficiente angular da reta que passa pelos pontos A e B, considere as seguintes afirmações:
I. O coeficiente angular  é igual a 2.
é igual a 2.
II. O coeficiente angular  é igual a − 3.
é igual a − 3.
III. O coeficiente angular  é igual a 1.
é igual a 1.
IV. O coeficiente angular  é igual a − 2.
é igual a − 2.
Nessas condições, está correto o que se afirma em
 indica o coeficiente angular da reta que passa pelos pontos A e B, considere as seguintes afirmações:
indica o coeficiente angular da reta que passa pelos pontos A e B, considere as seguintes afirmações:
 é igual a 2.
é igual a 2. é igual a − 3.
é igual a − 3. é igual a 1.
é igual a 1. é igual a − 2.
é igual a − 2.
Observe a figura (fora de escala). Podemos afirmar que a equação reduzida da reta MN é
Dados:
O ângulo 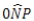 mede 45°
mede 45°
O Segmento 0P mede √8
O ângulo 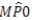 mede 90°
mede 90°
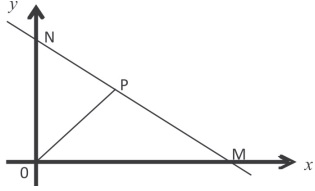
Observe a figura (fora de escala). Podemos afirmar que a equação reduzida da reta MN é
Dados:
O ângulo
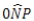 mede 45°
mede 45° O Segmento 0P mede √8
O ângulo
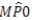 mede 90°
mede 90°
A equação da reta bissetriz do menor ângulo formado pelas retas x – 2y = 0 e 2x – y = 0 é dada por
As duas retas r: y = - x + 3 e s: y = x + k interceptam-se no ponto (1,2). A Área do triângulo formado pelas retas r e s e pelo eixo y é:
No plano cartesiano usual, a área, em unidade de área (u.a), do triângulo cujos três lados estão respectivamente sobre as retas de equações
x + y – 5 = 0; 3x – 2y + 5 = 0 e 2x – 3y + 5 = 0 é
x + y – 5 = 0; 3x – 2y + 5 = 0 e 2x – 3y + 5 = 0 é
No plano cartesiano, a reta de equação 2 x - 3 y = 12 intercepta os eixos coordenados nos pontos A e B. O ponto médio do segmento AB tem coordenadas
Se P é o ponto de intersecção das retas de equações  , a área do triângulo de vértices A(0, 3), B(2, 0) e P é
, a área do triângulo de vértices A(0, 3), B(2, 0) e P é
 , a área do triângulo de vértices A(0, 3), B(2, 0) e P é
, a área do triângulo de vértices A(0, 3), B(2, 0) e P é




São dados, no plano cartesiano, o ponto P de coordenadas ( 3, 6 ) e a circunferência C de equação ( x - 1 )2 + ( y - 2 )2 = 1 . Uma reta t passa por P e é tangente a C em um ponto Q. Então a distância de P a Q é





Se traçarmos essa circunferência, o seu comprimento, em u.c., será;
