Questõessobre Equação e Inequação Logarítmica
Se n é um número natural, a solução da
equação 9 – 2x – 2x–1 – 2x–2 – .... – 2x–n – ....= 0 é
A equação 2 log x = log 1000 + colog 10 existe para x igual a
Se log2(8m) = 5 e log3 (n/2) = 2 , então os valores de m e n são, respectivamente,
Se x
≠ y são reais não negativos e
log(x²
+ y²)
= 2 · log(x + y) , o valor de
xy
+ yx
é igual a:
Observe uma propriedade muito útil para reduzir cálculos que envolvem logaritmos.
logba ∙ logc b = logca, com a, b e c reais tais que a > 0, b > 0 e c > 0, com b ≠ 1 e c ≠ 1.
Aplicando essa propriedade sucessivamente, o valor da expressão log916 ∙ log59 ∙ log45 é
Observe uma propriedade muito útil para reduzir cálculos que envolvem logaritmos.
logba ∙ logc b = logca, com a, b e c reais tais que a > 0, b > 0 e c > 0, com b ≠ 1 e c ≠ 1.
Aplicando essa propriedade sucessivamente, o valor da expressão log916 ∙ log59 ∙ log45 é
Desenvolvida em 1935 por Charles F. Richter, com a colaboração de Beno Gutenberg, a escala Richter permite determinar a magnitude (M) de um terremoto, fenômeno que libera
uma grande quantidade de energia (E) que se propaga pela
Terra em todas as direções. A magnitude e a energia de um
terremoto podem ser relacionadas pela expressão a seguir,
em que E é expressa em erg, uma unidade de medida de
energia do sistema CGS.
logE = 11,8 + 1,5M
A tabela apresenta os efeitos gerados por um terremoto, de
acordo com sua magnitude na escala Richter:

No dia 6 de janeiro de 2020, o sul de Porto Rico foi atingido por um terremoto que liberou uma quantidade de energia
E = 1013,8 J. Considerando a tabela e que 1 erg = 10–7
J, esse
terremoto

Se log4 x + log8 x = 1, então o valor de x é



O valor da expressão 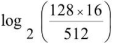 é
é
O valor da expressão 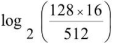 é
é
Se x e são números reais positivos e ambos
diferentes de um, então, o valor de xu , onde  é igual a
é igual a

Se x e são números reais positivos e ambos
diferentes de um, então, o valor de xu , onde  é igual a
é igual a


A solução da inequação log2 (x-1) < log 2 (x-2) +1 é
o resolver a equação 3 2X - 7 . 3X + 12 = 0, dados log2 = 0,30 e log3=0,48, a solução é
Considerando ln 10 = 2,3, então o valor da expressão  é igual a:
é igual a:
Considerando ln 10 = 2,3, então o valor da expressão  é igual a:
é igual a:
Considere as afirmações abaixo.
I - A equação log10x = 10x
tem, pelo menos,
uma solução real.
II - Para todo número real x , √x² = x .
III - A equação (x + 2)
2√x-2 = log10(1 − x)
não tem soluções reais.
Assinale a alternativa que contém a(s)
afirmação(ões) correta(s).
Considere as afirmações abaixo.
I - A equação log10x = 10x tem, pelo menos, uma solução real.
II - Para todo número real x , √x² = x .
III - A equação (x + 2) 2√x-2 = log10(1 − x) não tem soluções reais.
Assinale a alternativa que contém a(s)
afirmação(ões) correta(s).
Sejam números reais
positivos, tais que
números reais
positivos, tais que e
e . O valor da expressão
. O valor da expressão é igual a:
é igual a:
Sejam números reais
positivos, tais que
números reais
positivos, tais que e
e . O valor da expressão
. O valor da expressão é igual a:
é igual a:
Considerando log(2x + y) = log a2 e log a = 4,
então loga
[(x + y)2 - x2
].y-1 é igual a
Considere a seguinte tabela, em que ln( )x representa o logaritmo neperiano de x :

O valor de x que satisfaz a equação 6x =10 x
é aproximadamente igual a
Considere a seguinte tabela, em que ln( )x representa o logaritmo neperiano de x :

O valor de x que satisfaz a equação 6x =10 x
é aproximadamente igual a
Aequação log4 (x+3)2 + log2( x -4)= log2 (3x - 7) tem para
solução
O valor de x que satisfaz a equação 16log2x . x-2 =1024 é igual a
Sendo n o número de soluções reais da equação log15  então:
então:
Sendo n o número de soluções reais da equação log15  então:
então: