a1fe3de6-ab
ENEM 2023 - Matemática - Ângulos - Lei Angular de Thales, Áreas e Perímetros, Geometria Plana, Raciocínio Lógico, Relações Métricas no Triângulo Retângulo, Triângulos
Sejam a, b e c as medidas dos lados de um triângulo
retângulo, tendo a como medida da hipotenusa. Esses
valores a, b e c são, respectivamente, os diâmetros dos
círculos C1
, C2
e C3, como apresentados na figura.
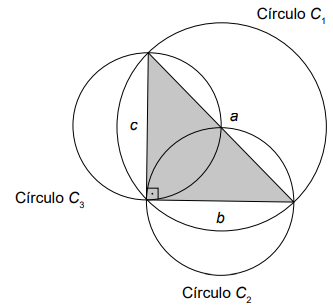
Observe que essa construção assegura, pelo teorema
de Pitágoras, que área (C1
) = área (C2
) + área (C3
).
Um professor de matemática era conhecedor dessa
construção e, confraternizando com dois amigos em uma
pizzaria onde são vendidas pizzas somente em formato
de círculo, lançou um desafio: mesmo sem usar um
instrumento de medição, poderia afirmar com certeza se
a área do círculo correspondente à pizza que ele pedisse
era maior, igual ou menor do que a soma das áreas das
pizzas dos dois amigos. Assim, foram pedidas três pizzas.
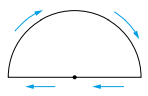
O professor as dividiu ao meio e formou um triângulo com
os diâmetros das pizzas, conforme indicado na figura.
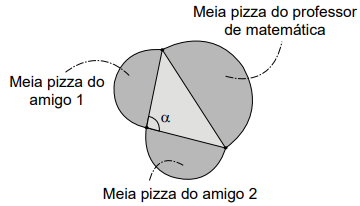
A partir da medida do ângulo α, o professor afirmou
que a área de sua pizza é maior do que a soma das áreas
das outras duas pizzas.
A área da pizza do professor de matemática é maior do
que a soma das áreas das outras duas pizzas, pois
Sejam a, b e c as medidas dos lados de um triângulo
retângulo, tendo a como medida da hipotenusa. Esses
valores a, b e c são, respectivamente, os diâmetros dos
círculos C1
, C2
e C3, como apresentados na figura.

Observe que essa construção assegura, pelo teorema
de Pitágoras, que área (C1
) = área (C2
) + área (C3
).
Um professor de matemática era conhecedor dessa
construção e, confraternizando com dois amigos em uma
pizzaria onde são vendidas pizzas somente em formato
de círculo, lançou um desafio: mesmo sem usar um
instrumento de medição, poderia afirmar com certeza se
a área do círculo correspondente à pizza que ele pedisse
era maior, igual ou menor do que a soma das áreas das
pizzas dos dois amigos. Assim, foram pedidas três pizzas.
O professor as dividiu ao meio e formou um triângulo com
os diâmetros das pizzas, conforme indicado na figura.

A partir da medida do ângulo α, o professor afirmou
que a área de sua pizza é maior do que a soma das áreas
das outras duas pizzas.
A área da pizza do professor de matemática é maior do
que a soma das áreas das outras duas pizzas, pois
A
0° < α < 90°
B
α = 90°
C
90° < α < 180°
D
α = 180°
E
180° < α < 360°