Questõesde ENEM 2019 sobre Matemática
A ingestão de sódio no Brasil, que já é normalmente
alta, tende a atingir os mais elevados índices no
inverno, quando cresce o consumo de alimentos
calóricos e condimentados. Mas, o sal não é um vilão,
ele pode e deve ser consumido diariamente, salvo
algumas restrições. Para uma pessoa saudável, o
consumo máximo de sal de cozinha (cloreto de sódio)
não deve ultrapassar 6 g diárias ou 2,4 g de sódio,
considerando que o sal de cozinha é composto por
40% de sódio e 60% de cloro.
Disponível em: http://depoisdos25.com.
Acesso em: 31 jul. 2012 (adaptado).
Considere uma pessoa saudável que, no decorrer de
30 dias, consuma 450 g de sal de cozinha.
O seu consumo médio diário excede ao consumo
máximo recomendado diariamente em
Um asteroide batizado de 2013-TV135 passou
a aproximadamente 6,7 × 106 quilômetros da Terra.
A presença do objeto espacial nas proximidades
da Terra foi detectada por astrônomos ucranianos,
que alertaram para uma possível volta do asteroide
em 2032.
Disponível em: www1.folha.uol.com.br. Acesso em: 30 out. 2013.
O valor posicional do algarismo 7, presente na notação
científica da distância, em quilômetro, entre o asteroide
e a Terra, corresponde a
As coordenadas usualmente utilizadas na localização
de um ponto sobre a superfície terrestre são a latitude
e a longitude. Para tal, considera-se que a Terra tem a
forma de uma esfera.
Um meridiano é uma circunferência sobre a
superfície da Terra que passa pelos polos Norte e Sul,
representados na figura por PN e PS. O comprimento
da semicircunferência que une os pontos PN e PS tem
comprimento igual a 20 016 km. A linha do Equador
também é uma circunferência sobre a superfície da
Terra, com raio igual ao da Terra, sendo que o plano
que a contém é perpendicular ao que contém qualquer
meridiano.
Seja P um ponto na superfície da Terra, C o centro
da Terra e o segmento  um raio, conforme mostra a
figura. Seja ϕ o ângulo que o segmento
um raio, conforme mostra a
figura. Seja ϕ o ângulo que o segmento  faz com
o plano que contém a linha do Equador. A medida em
graus de ϕ é a medida da latitude de P.
faz com
o plano que contém a linha do Equador. A medida em
graus de ϕ é a medida da latitude de P.
 Suponha que a partir da linha do Equador um navio
viaja subindo em direção ao Polo Norte, percorrendo um
meridiano, até um ponto P com 30 graus de latitude.
Suponha que a partir da linha do Equador um navio
viaja subindo em direção ao Polo Norte, percorrendo um
meridiano, até um ponto P com 30 graus de latitude.
Quantos quilômetros são percorridos pelo navio?
 um raio, conforme mostra a
figura. Seja ϕ o ângulo que o segmento
um raio, conforme mostra a
figura. Seja ϕ o ângulo que o segmento  faz com
o plano que contém a linha do Equador. A medida em
graus de ϕ é a medida da latitude de P.
faz com
o plano que contém a linha do Equador. A medida em
graus de ϕ é a medida da latitude de P.
O boliche é um esporte cujo objetivo é derrubar, com
uma bola, uma série de pinos alinhados em uma pista.
A professora de matemática organizou um jogo de
boliche em que os pinos são garrafas que possuem
rótulos com números, conforme mostra o esquema.

O aluno marca pontos de acordo com a soma das
quantidades expressas nos rótulos das garrafas que
são derrubadas. Se dois ou mais rótulos representam
a mesma quantidade, apenas um deles entra na
contagem dos pontos. Um aluno marcou 7,55 pontos em
uma jogada. Uma das garrafas que ele derrubou tinha o
rótulo 6,8.
A quantidade máxima de garrafas que ele derrubou para
obter essa pontuação é igual a

Um grupo de engenheiros está projetando um motor
cujo esquema de deslocamento vertical do pistão dentro
da câmara de combustão está representado na figura.

A função h(t) = 4 + 4sen (βt /2 - π/2) definida para t ≥ 0
descreve como varia a altura h, medida em centímetro, da
parte superior do pistão dentro da câmara de combustão,
em função do tempo t, medido em segundo. Nas figuras
estão indicadas as alturas do pistão em dois instantes
distintos.
O valor do parâmetro β , que é dado por um número
inteiro positivo, está relacionado com a velocidade
de deslocamento do pistão. Para que o motor tenha
uma boa potência, é necessário e suficiente que, em
menos de 4 segundos após o início do funcionamento
(instante t = 0), a altura da base do pistão alcance por
três vezes o valor de 6 cm. Para os cálculos, utilize 3
como aproximação para π.
O menor valor inteiro a ser atribuído ao parâmetro β , de
forma que o motor a ser construído tenha boa potência, é
Um grupo de engenheiros está projetando um motor cujo esquema de deslocamento vertical do pistão dentro da câmara de combustão está representado na figura.

A função h(t) = 4 + 4sen (βt /2 - π/2) definida para t ≥ 0 descreve como varia a altura h, medida em centímetro, da parte superior do pistão dentro da câmara de combustão, em função do tempo t, medido em segundo. Nas figuras estão indicadas as alturas do pistão em dois instantes distintos.
O valor do parâmetro β , que é dado por um número inteiro positivo, está relacionado com a velocidade de deslocamento do pistão. Para que o motor tenha uma boa potência, é necessário e suficiente que, em menos de 4 segundos após o início do funcionamento (instante t = 0), a altura da base do pistão alcance por três vezes o valor de 6 cm. Para os cálculos, utilize 3 como aproximação para π.
O menor valor inteiro a ser atribuído ao parâmetro β , de
forma que o motor a ser construído tenha boa potência, é
Para construir uma piscina, cuja área total da
superfície interna é igual a 40 m2, uma construtora
apresentou o seguinte orçamento:
• R$ 10 000,00 pela elaboração do projeto;
• R$ 40 000,00 pelos custos fixos;
• R$ 2 500,00 por metro quadrado para construção
da área interna da piscina.
Após a apresentação do orçamento, essa empresa
decidiu reduzir o valor de elaboração do projeto em
50%, mas recalculou o valor do metro quadrado para a
construção da área interna da piscina, concluindo haver
a necessidade de aumentá-lo em 25%. Além disso, a
construtora pretende dar um desconto nos custos fixos,
de maneira que o novo valor do orçamento seja reduzido
em 10% em relação ao total inicial.
O percentual de desconto que a construtora deverá
conceder nos custos fixos é de
Para construir uma piscina, cuja área total da superfície interna é igual a 40 m2, uma construtora apresentou o seguinte orçamento:
• R$ 10 000,00 pela elaboração do projeto;
• R$ 40 000,00 pelos custos fixos;
• R$ 2 500,00 por metro quadrado para construção da área interna da piscina.
Após a apresentação do orçamento, essa empresa decidiu reduzir o valor de elaboração do projeto em 50%, mas recalculou o valor do metro quadrado para a construção da área interna da piscina, concluindo haver a necessidade de aumentá-lo em 25%. Além disso, a construtora pretende dar um desconto nos custos fixos, de maneira que o novo valor do orçamento seja reduzido em 10% em relação ao total inicial.
O percentual de desconto que a construtora deverá
conceder nos custos fixos é de
Uma construtora pretende conectar um reservatório
central (Rc) em formato de um cilindro, com raio interno
igual a 2 m e altura interna igual a 3,30 m, a quatro
reservatórios cilíndricos auxiliares (R1, R2, R3 e R4),
os quais possuem raios internos e alturas internas
medindo 1,5 m.

As ligações entre o reservatório central e os
auxiliares são feitas por canos cilíndricos com 0,10 m
de diâmetro interno e 20 m de comprimento, conectados
próximos às bases de cada reservatório. Na conexão
de cada um desses canos com o reservatório central há
registros que liberam ou interrompem o fluxo de água.
No momento em que o reservatório central está
cheio e os auxiliares estão vazios, abrem-se os quatro
registros e, após algum tempo, as alturas das colunas
de água nos reservatórios se igualam, assim que cessa
o fluxo de água entre eles, pelo princípio dos vasos
comunicantes.
A medida, em metro, das alturas das colunas de água
nos reservatórios auxiliares, após cessar o fluxo de
água entre eles, é
Uma construtora pretende conectar um reservatório central (Rc) em formato de um cilindro, com raio interno igual a 2 m e altura interna igual a 3,30 m, a quatro reservatórios cilíndricos auxiliares (R1, R2, R3 e R4), os quais possuem raios internos e alturas internas medindo 1,5 m.

As ligações entre o reservatório central e os auxiliares são feitas por canos cilíndricos com 0,10 m de diâmetro interno e 20 m de comprimento, conectados próximos às bases de cada reservatório. Na conexão de cada um desses canos com o reservatório central há registros que liberam ou interrompem o fluxo de água.
No momento em que o reservatório central está cheio e os auxiliares estão vazios, abrem-se os quatro registros e, após algum tempo, as alturas das colunas de água nos reservatórios se igualam, assim que cessa o fluxo de água entre eles, pelo princípio dos vasos comunicantes.
A medida, em metro, das alturas das colunas de água
nos reservatórios auxiliares, após cessar o fluxo de
água entre eles, é
A taxa de urbanização de um município é dada pela razão entre a população urbana e a população total do
município (isto é, a soma das populações rural e urbana). Os gráficos apresentam, respectivamente, a população
urbana e a população rural de cinco municípios (I, II, III, IV, V) de uma mesma região estadual. Em reunião
entre o governo do estado e os prefeitos desses municípios, ficou acordado que o município com maior taxa de
urbanização receberá um investimento extra em infraestrutura.

Segundo o acordo, qual município receberá o investimento extra?
A taxa de urbanização de um município é dada pela razão entre a população urbana e a população total do município (isto é, a soma das populações rural e urbana). Os gráficos apresentam, respectivamente, a população urbana e a população rural de cinco municípios (I, II, III, IV, V) de uma mesma região estadual. Em reunião entre o governo do estado e os prefeitos desses municípios, ficou acordado que o município com maior taxa de urbanização receberá um investimento extra em infraestrutura.

Segundo o acordo, qual município receberá o investimento extra?
Em um determinado ano, os computadores da receita federal de um país identificaram como inconsistentes
20% das declarações de imposto de renda que lhe foram encaminhadas. Uma declaração é classificada como
inconsistente quando apresenta algum tipo de erro ou conflito nas informações prestadas. Essas declarações
consideradas inconsistentes foram analisadas pelos auditores, que constataram que 25% delas eram fraudulentas.
Constatou-se ainda que, dentre as declarações que não apresentaram inconsistências, 6,25% eram fraudulentas.
Qual é a probabilidade de, nesse ano, a declaração de um contribuinte ser considerada inconsistente, dado que
ela era fraudulenta?
Em um determinado ano, os computadores da receita federal de um país identificaram como inconsistentes 20% das declarações de imposto de renda que lhe foram encaminhadas. Uma declaração é classificada como inconsistente quando apresenta algum tipo de erro ou conflito nas informações prestadas. Essas declarações consideradas inconsistentes foram analisadas pelos auditores, que constataram que 25% delas eram fraudulentas. Constatou-se ainda que, dentre as declarações que não apresentaram inconsistências, 6,25% eram fraudulentas.
Qual é a probabilidade de, nesse ano, a declaração de um contribuinte ser considerada inconsistente, dado que ela era fraudulenta?
Um comerciante, que vende somente pastel, refrigerante em lata e caldo de cana em copos, fez um levantamento
das vendas realizadas durante a semana. O resultado desse levantamento está apresentado no gráfico.

Ele estima que venderá, em cada dia da próxima semana, uma quantidade de refrigerante em lata igual à
soma das quantidades de refrigerante em lata e caldo de cana em copos vendidas no respectivo dia da última
semana. Quanto aos pastéis, estima vender, a cada dia da próxima semana, uma quantidade igual à quantidade
de refrigerante em lata que prevê vender em tal dia. Já para o número de caldo de cana em copos, estima que as
vendas diárias serão iguais às da última semana.
Segundo essas estimativas, a quantidade a mais de pastéis que esse comerciante deve vender na próxima semana é
Um comerciante, que vende somente pastel, refrigerante em lata e caldo de cana em copos, fez um levantamento das vendas realizadas durante a semana. O resultado desse levantamento está apresentado no gráfico.

Ele estima que venderá, em cada dia da próxima semana, uma quantidade de refrigerante em lata igual à soma das quantidades de refrigerante em lata e caldo de cana em copos vendidas no respectivo dia da última semana. Quanto aos pastéis, estima vender, a cada dia da próxima semana, uma quantidade igual à quantidade de refrigerante em lata que prevê vender em tal dia. Já para o número de caldo de cana em copos, estima que as vendas diárias serão iguais às da última semana.
Segundo essas estimativas, a quantidade a mais de pastéis que esse comerciante deve vender na próxima semana é
Um aplicativo de relacionamentos funciona da
seguinte forma: o usuário cria um perfil com foto e
informações pessoais, indica as características dos
usuários com quem deseja estabelecer contato e
determina um raio de abrangência a partir da sua
localização. O aplicativo identifica as pessoas que se
encaixam no perfil desejado e que estão a uma distância
do usuário menor ou igual ao raio de abrangência.
Caso dois usuários tenham perfis compatíveis e estejam
numa região de abrangência comum a ambos, o
aplicativo promove o contato entre os usuários, o que é
chamado de match.
O usuário P define um raio de abrangência com
medida de 3 km e busca ampliar a possibilidade de
obter um match se deslocando para a região central da
cidade, que concentra um maior número de usuários.
O gráfico ilustra alguns bares que o usuário P costuma
frequentar para ativar o aplicativo, indicados por
I, II, III, IV e V. Sabe-se que os usuários Q, R e S,
cujas posições estão descritas pelo gráfico, são
compatíveis com o usuário P, e que estes definiram
raios de abrangência respectivamente iguais a
3 km, 2 km e 5 km.

Com base no gráfico e nas afirmações anteriores, em
qual bar o usuário P teria a possibilidade de um match
com os usuários Q, R e S, simultaneamente?
Um aplicativo de relacionamentos funciona da seguinte forma: o usuário cria um perfil com foto e informações pessoais, indica as características dos usuários com quem deseja estabelecer contato e determina um raio de abrangência a partir da sua localização. O aplicativo identifica as pessoas que se encaixam no perfil desejado e que estão a uma distância do usuário menor ou igual ao raio de abrangência. Caso dois usuários tenham perfis compatíveis e estejam numa região de abrangência comum a ambos, o aplicativo promove o contato entre os usuários, o que é chamado de match.
O usuário P define um raio de abrangência com medida de 3 km e busca ampliar a possibilidade de obter um match se deslocando para a região central da cidade, que concentra um maior número de usuários. O gráfico ilustra alguns bares que o usuário P costuma frequentar para ativar o aplicativo, indicados por I, II, III, IV e V. Sabe-se que os usuários Q, R e S, cujas posições estão descritas pelo gráfico, são compatíveis com o usuário P, e que estes definiram raios de abrangência respectivamente iguais a 3 km, 2 km e 5 km.

Com base no gráfico e nas afirmações anteriores, em
qual bar o usuário P teria a possibilidade de um match
com os usuários Q, R e S, simultaneamente?
Uma empresa tem diversos funcionários. Um deles
é o gerente, que recebe R$ 1 000,00 por semana.
Os outros funcionários são diaristas. Cada um deles
trabalha 2 dias por semana, recebendo R$ 80,00 por
dia trabalhado.
Chamando de X a quantidade total de funcionários
da empresa, a quantia Y, em reais, que esta empresa
gasta semanalmente para pagar seus funcionários é
expressa por
Uma empresa tem diversos funcionários. Um deles é o gerente, que recebe R$ 1 000,00 por semana. Os outros funcionários são diaristas. Cada um deles trabalha 2 dias por semana, recebendo R$ 80,00 por dia trabalhado.
Chamando de X a quantidade total de funcionários da empresa, a quantia Y, em reais, que esta empresa gasta semanalmente para pagar seus funcionários é expressa por
Os alunos de uma turma escolar foram divididos em
dois grupos. Um grupo jogaria basquete, enquanto o
outro jogaria futebol. Sabe-se que o grupo de basquete
é formado pelos alunos mais altos da classe e tem
uma pessoa a mais do que o grupo de futebol. A tabela
seguinte apresenta informações sobre as alturas dos
alunos da turma.
Média Mediana Moda
1,65 1,67 1,70
Os alunos P, J, F e M medem, respectivamente,
1,65 m, 1,66 m, 1,67 m e 1,68 m, e as suas alturas não
são iguais a de nenhum outro colega da sala.
Segundo essas informações, argumenta-se que os
alunos P, J, F e M jogaram, respectivamente,
Os alunos de uma turma escolar foram divididos em dois grupos. Um grupo jogaria basquete, enquanto o outro jogaria futebol. Sabe-se que o grupo de basquete é formado pelos alunos mais altos da classe e tem uma pessoa a mais do que o grupo de futebol. A tabela seguinte apresenta informações sobre as alturas dos alunos da turma.
Média Mediana Moda
1,65 1,67 1,70
Os alunos P, J, F e M medem, respectivamente, 1,65 m, 1,66 m, 1,67 m e 1,68 m, e as suas alturas não são iguais a de nenhum outro colega da sala.
Segundo essas informações, argumenta-se que os
alunos P, J, F e M jogaram, respectivamente,
Construir figuras de diversos tipos, apenas
dobrando e cortando papel, sem cola e sem tesoura, é
a arte do origami (ori = dobrar; kami = papel), que tem
um significado altamente simbólico no Japão. A base
do origami é o conhecimento do mundo por base do
tato. Uma jovem resolveu construir um cisne usando
a técnica do origami, utilizando uma folha de papel de
18 cm por 12 cm. Assim, começou por dobrar a folha
conforme a figura.

Após essa primeira dobradura, a medida do segmento
AE é
Construir figuras de diversos tipos, apenas dobrando e cortando papel, sem cola e sem tesoura, é a arte do origami (ori = dobrar; kami = papel), que tem um significado altamente simbólico no Japão. A base do origami é o conhecimento do mundo por base do tato. Uma jovem resolveu construir um cisne usando a técnica do origami, utilizando uma folha de papel de 18 cm por 12 cm. Assim, começou por dobrar a folha conforme a figura.

Após essa primeira dobradura, a medida do segmento
AE é
O álcool é um depressor do sistema nervoso central
e age diretamente em diversos órgãos. A concentração
de álcool no sangue pode ser entendida como a razão
entre a quantidade q de álcool ingerido, medida em
grama, e o volume de sangue, em litro, presente no
organismo do indivíduo. Em geral, considera-se que
esse volume corresponda ao valor numérico dado
por 8% da massa corporal m desse indivíduo, medida
em quilograma.
De acordo com a Associação Médica Americana,
uma concentração alcoólica superior a 0,4 grama por
litro de sangue é capaz de trazer prejuízos à saúde do
indivíduo.
Disponível em: http://cisa.org.br. Acesso em: 1 dez. 2018 (adaptado)
A expressão relacionando q e m que representa a
concentração alcoólica prejudicial à saúde do indivíduo,
de acordo com a Associação Médica Americana, é
O álcool é um depressor do sistema nervoso central e age diretamente em diversos órgãos. A concentração de álcool no sangue pode ser entendida como a razão entre a quantidade q de álcool ingerido, medida em grama, e o volume de sangue, em litro, presente no organismo do indivíduo. Em geral, considera-se que esse volume corresponda ao valor numérico dado por 8% da massa corporal m desse indivíduo, medida em quilograma.
De acordo com a Associação Médica Americana, uma concentração alcoólica superior a 0,4 grama por litro de sangue é capaz de trazer prejuízos à saúde do indivíduo.
Disponível em: http://cisa.org.br. Acesso em: 1 dez. 2018 (adaptado)
A expressão relacionando q e m que representa a
concentração alcoólica prejudicial à saúde do indivíduo,
de acordo com a Associação Médica Americana, é
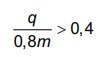
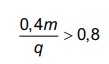
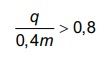
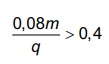
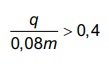
Um mestre de obras deseja fazer uma laje com
espessura de 5 cm utilizando concreto usinado,
conforme as dimensões do projeto dadas na figura.
O concreto para fazer a laje será fornecido por uma
usina que utiliza caminhões com capacidades máximas
de 2 m3, 5 m3 e 10 m3 de concreto.

Qual a menor quantidade de caminhões, utilizando suas
capacidades máximas, que o mestre de obras deverá
pedir à usina de concreto para fazer a laje?
Um mestre de obras deseja fazer uma laje com espessura de 5 cm utilizando concreto usinado, conforme as dimensões do projeto dadas na figura. O concreto para fazer a laje será fornecido por uma usina que utiliza caminhões com capacidades máximas de 2 m3, 5 m3 e 10 m3 de concreto.

Qual a menor quantidade de caminhões, utilizando suas
capacidades máximas, que o mestre de obras deverá
pedir à usina de concreto para fazer a laje?
O Índice de Desenvolvimento Humano (IDH) é uma
medida usada para classificar os países pelo seu grau
de desenvolvimento. Para seu cálculo, são levados em
consideração a expectativa de vida ao nascer, tempo de
escolaridade e renda per capita, entre outros. O menor
valor deste índice é zero e o maior é um. Cinco países
foram avaliados e obtiveram os seguintes índices de
desenvolvimento humano: o primeiro país recebeu um
valor X , o segundo √X , o terceiro X1/3, o quarto X2 e o
último X3. Nenhum desses países zerou ou atingiu o
índice máximo.
Qual desses países obteve o maior IDH?
O Índice de Desenvolvimento Humano (IDH) é uma medida usada para classificar os países pelo seu grau de desenvolvimento. Para seu cálculo, são levados em consideração a expectativa de vida ao nascer, tempo de escolaridade e renda per capita, entre outros. O menor valor deste índice é zero e o maior é um. Cinco países foram avaliados e obtiveram os seguintes índices de desenvolvimento humano: o primeiro país recebeu um valor X , o segundo √X , o terceiro X1/3, o quarto X2 e o último X3. Nenhum desses países zerou ou atingiu o índice máximo.
Qual desses países obteve o maior IDH?
O Sistema Métrico Decimal é o mais utilizado
atualmente para medir comprimentos e distâncias.
Em algumas atividades, porém, é possível observar
a utilização de diferentes unidades de medida.
Um exemplo disso pode ser observado no quadro.
Unidade Equivalência
Polegada 2,54 centímetros
Jarda 3 pés
Jarda 0,9144 metro
Assim, um pé, em polegada, equivale a
O Sistema Métrico Decimal é o mais utilizado atualmente para medir comprimentos e distâncias. Em algumas atividades, porém, é possível observar a utilização de diferentes unidades de medida. Um exemplo disso pode ser observado no quadro.
Unidade Equivalência
Polegada 2,54 centímetros
Jarda 3 pés
Jarda 0,9144 metro
Assim, um pé, em polegada, equivale a
Em uma fábrica de refrigerantes, é necessário
que se faça periodicamente o controle no processo
de engarrafamento para evitar que sejam envasadas
garrafas fora da especificação do volume escrito no rótulo.
Diariamente, durante 60 dias, foram anotadas as
quantidades de garrafas fora dessas especificações.
O resultado está apresentado no quadro.
A média diária de garrafas fora das especificações no
período considerado é
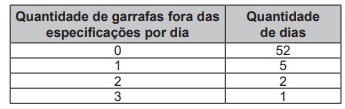
Em uma fábrica de refrigerantes, é necessário que se faça periodicamente o controle no processo de engarrafamento para evitar que sejam envasadas garrafas fora da especificação do volume escrito no rótulo.
Diariamente, durante 60 dias, foram anotadas as quantidades de garrafas fora dessas especificações. O resultado está apresentado no quadro.

A média diária de garrafas fora das especificações no
período considerado é