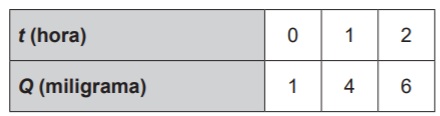
Em um município foi realizado um levantamento
relativo ao número de médicos, obtendo-se os dados:

Tendo em vista a crescente demanda por atendimento
médico na rede de saúde pública, pretende-se
promover a expansão, a longo prazo, do número de
médicos desse município, seguindo o comportamento
de crescimento linear no período observado no quadro.
Qual a previsão do número de médicos nesse município
para o ano 2040?
Em um município foi realizado um levantamento relativo ao número de médicos, obtendo-se os dados:

Tendo em vista a crescente demanda por atendimento médico na rede de saúde pública, pretende-se promover a expansão, a longo prazo, do número de médicos desse município, seguindo o comportamento de crescimento linear no período observado no quadro.
Qual a previsão do número de médicos nesse município
para o ano 2040?