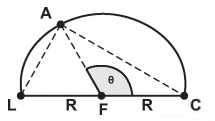
Um jovem lança uma bola de borracha para observar
sua trajetória e altura h (em metros) atingida ao longo
de um certo intervalo de tempo t (em segundos). Nesse
intervalo, a bola quica no chão algumas vezes, perdendo
altura progressivamente. Parte de sua trajetória está
descrita na figura a seguir.

Em suas observações, quantas vezes o jovem pôde
constatar que a bola atingiu a marca de 35 metros?
Um jovem lança uma bola de borracha para observar sua trajetória e altura h (em metros) atingida ao longo de um certo intervalo de tempo t (em segundos). Nesse intervalo, a bola quica no chão algumas vezes, perdendo altura progressivamente. Parte de sua trajetória está descrita na figura a seguir.

Em suas observações, quantas vezes o jovem pôde
constatar que a bola atingiu a marca de 35 metros?


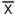 representa o número 10
x 1 000, ou seja, 10 000.
representa o número 10
x 1 000, ou seja, 10 000.
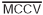 e
e
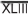 são, respectivamente, iguais aW
são, respectivamente, iguais aW


