Os medicamentos, imediatamente após a ingestão,
começam a ser metabolizados pelo organismo, o que
faz com que sua concentração no sangue diminua
gradualmente, num processo denominado decaimento.
Denomina-se meia-vida de uma substância o tempo
necessário para que o teor dessa substância no sangue
se reduza à metade do valor inicial.
Considere a situação em que um médico prescreveu a um
paciente uma dosagem de 800 mg de um medicamento
cuja meia-vida é 6 horas, com recomendação de tomar
um comprimido a cada 12 horas, durante 3 dias. Para
esse medicamento, considera-se superdosagem um teor
superior a 1 520 mg, o que causa riscos de intoxicação.
Apressado em recuperar-se a tempo de ir a uma festa,
o paciente sugeriu ao médico que mudasse a prescrição
para 6 em 6 horas, imaginando que, assim, reduziria
o tempo de tratamento. O médico contra-argumentou,
informando ao paciente que, caso antecipasse as doses,
correria o risco de estar intoxicado em
Os medicamentos, imediatamente após a ingestão, começam a ser metabolizados pelo organismo, o que faz com que sua concentração no sangue diminua gradualmente, num processo denominado decaimento. Denomina-se meia-vida de uma substância o tempo necessário para que o teor dessa substância no sangue se reduza à metade do valor inicial.
Considere a situação em que um médico prescreveu a um paciente uma dosagem de 800 mg de um medicamento cuja meia-vida é 6 horas, com recomendação de tomar um comprimido a cada 12 horas, durante 3 dias. Para esse medicamento, considera-se superdosagem um teor superior a 1 520 mg, o que causa riscos de intoxicação.
Apressado em recuperar-se a tempo de ir a uma festa, o paciente sugeriu ao médico que mudasse a prescrição para 6 em 6 horas, imaginando que, assim, reduziria o tempo de tratamento. O médico contra-argumentou, informando ao paciente que, caso antecipasse as doses, correria o risco de estar intoxicado em

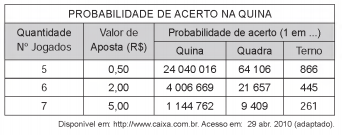
 o que mostra que Antônio tem mais chances
3114
de acertar.
o que mostra que Antônio tem mais chances
3114
de acertar. o que mostra que Antônio tem mais chances de acertar.
o que mostra que Antônio tem mais chances de acertar. o que mostra que José tem mais chances de acertar.
o que mostra que José tem mais chances de acertar. o que mostra que Antônio tem mais chances de acertar.
o que mostra que Antônio tem mais chances de acertar. o que mostra que José tem mais chances de acertar.
o que mostra que José tem mais chances de acertar.

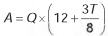 , onde
, onde