Na figura, os raios das circunferências
de centros M e N são, respectivamente,
2r e 5r. Se a área do quadrilátero AMBN
é 16√6, o valor de r é



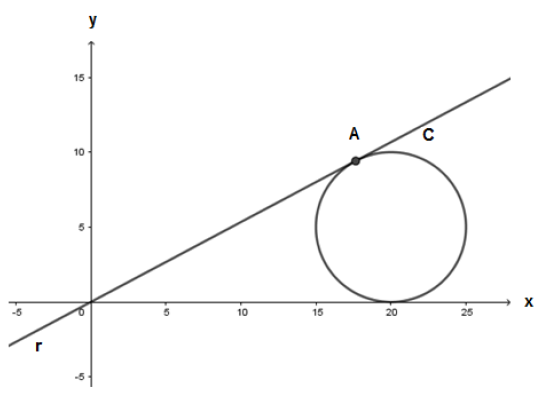
Dada a circunferência C: (x-20)² + (y-5)² = 25, a equação da reta r, que contém a origem e é tangente à circunferência C no ponto A , conforme figura abaixo, é

 do triângulo ABC vale 5√3/2 cm, o comprimento
da circunferência, em centímetros, é igual a
do triângulo ABC vale 5√3/2 cm, o comprimento
da circunferência, em centímetros, é igual a A linha curva indicada na figura tem extremidades em A e B e é formada apenas por semicircunferências. 
Se o comprimento de AB é igual a x ,então o comprimento da linha curva será igual a







2π + √3
Na figura, em que está representada a circunferência trigonométrica, P é a extremidade de um arco trigonométrico da 1a . volta cuja medida, em radianos, é igual a α. Observe que P é um ponto do 2o quadrante localizado no interior do retângulo ABCD.

As coordenadas dos vértices do retângulo são dadas por:

Assim, é necessariamente verdadeira a desigualdade







 é 300
metros, o tempo necessário para o grupo completar o
percurso é de:
é 300
metros, o tempo necessário para o grupo completar o
percurso é de:
 = 10 m. Do centro C ao plano horizontal
do chão, há uma distância de 11 m. Os pontos A e B, situados no mesmo plano vertical, ACB,
pertencem à circunferência dessa roda e distam, respectivamente, 16 m e 3,95 m do plano do
chão. Observe o esquema e a tabela:
= 10 m. Do centro C ao plano horizontal
do chão, há uma distância de 11 m. Os pontos A e B, situados no mesmo plano vertical, ACB,
pertencem à circunferência dessa roda e distam, respectivamente, 16 m e 3,95 m do plano do
chão. Observe o esquema e a tabela:
 corresponde a:
corresponde a:Assinale a proposição CORRETA.

Assinale a proposição CORRETA.
As circunferências C de equação
x2 + y2 - 2x - 10y + 22 = 0 e C’ de equação
x2 + y2 - 8x - 4y +10 = 0 são secantes.

Deseja-se construir um cilindro de altura h e raio r, em que e o volume V = 16 π cm3. Para tanto, deverá ser usada na construção da superfície lateral uma chapa metálica retangular de comprimento igual a