Infinitas circunferências são concêntricas, de raios r1
, r2
,
r
3
, …, com  . Sabendo que r1 = 1 cm,
a soma do comprimento de todas as circunferências é, em
cm, igual a:
. Sabendo que r1 = 1 cm,
a soma do comprimento de todas as circunferências é, em
cm, igual a:
Infinitas circunferências são concêntricas, de raios r1
, r2
,
r
3
, …, com  . Sabendo que r1 = 1 cm,
a soma do comprimento de todas as circunferências é, em
cm, igual a:
. Sabendo que r1 = 1 cm,
a soma do comprimento de todas as circunferências é, em
cm, igual a:


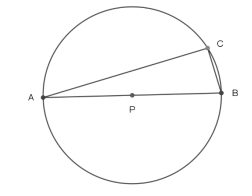




 está contido no 1o
quadrante, a
distância entre os pontos R e S é
está contido no 1o
quadrante, a
distância entre os pontos R e S é



