Questõessobre Circunferências e Círculos

Duas circunferências, de raios 12cm e 9cm, são tangentes a uma reta r, em lados opostos.
Se a distância entre os pontos de tangência P e Q é de 28cm, então a distância d entre
as circunferências mede

Duas circunferências, de raios 12cm e 9cm, são tangentes a uma reta r, em lados opostos.
Se a distância entre os pontos de tangência P e Q é de 28cm, então a distância d entre
as circunferências mede
Nas competições olímpicas de Tiro com Arco, o alvo possui
1,22 m de diâmetro. Ele é formado por dez circunferências
concêntricas pintadas sobre um mesmo plano e a uma
distância constante de 6,1 cm entre si, como vemos no
esquema.

Podemos afirmar corretamente que a razão entre a área da
região cinza e a área total do alvo, nessa ordem, é igual a
Nas competições olímpicas de Tiro com Arco, o alvo possui 1,22 m de diâmetro. Ele é formado por dez circunferências concêntricas pintadas sobre um mesmo plano e a uma distância constante de 6,1 cm entre si, como vemos no esquema.

A moeda de um real que entrou em
circulação em 1º de julho de 1994 possuía um
diâmetro de 24,0 mm. Devido a alguns fatores foi
lançada uma nova moeda de um real em 1º de Julho
de 1998, com 27,0 mm de diâmetro, a qual usamos
até hoje. O aumento do raio da moeda foi de:
Se D é um disco de raio r no plano xOy, então ∫∫D dxdy = 2r.
O valor que expressa a área da superfície de uma esfera de raio R é o mesmo que expressa a área da
superfície de um círculo de raio r/2. Qual das alternativas indica corretamente a razão entre os raios r e
R?
Durante o pôr do Sol, entre o instante em que o disco solar encosta no horizonte e sua ocultação completa
decorrem, aproximadamente, 2 minutos.
A partir desse dado, assinale a alternativa que apresenta, corretamente, o diâmetro angular aparente do
Sol visto da Terra.
Durante o pôr do Sol, entre o instante em que o disco solar encosta no horizonte e sua ocultação completa decorrem, aproximadamente, 2 minutos.
A partir desse dado, assinale a alternativa que apresenta, corretamente, o diâmetro angular aparente do Sol visto da Terra.
No centro de uma pista de dança, foi construído um mosaico de led de 3 m × 3 m, dividido em nove
quadrados de lado 1 m. Em dois desses quadrados, foram inscritas duas circunferências, de acordo com
a figura a seguir.

Assinale a alternativa que apresenta, corretamente, a menor distância entre as duas circunferências
No centro de uma pista de dança, foi construído um mosaico de led de 3 m × 3 m, dividido em nove quadrados de lado 1 m. Em dois desses quadrados, foram inscritas duas circunferências, de acordo com a figura a seguir.

Assinale a alternativa que apresenta, corretamente, a menor distância entre as duas circunferências
Henrique começou a praticar tiro esportivo e treina em um alvo circular com 40 centímetros de diâmetro máximo, com 10 círculos concêntricos, ou seja, de mesmo centro, cujos raios podem ser identificados na ilustração que segue.

Considerando que Henrique ainda é um amador no esporte, a probabilidade de ele acertar o alvo é de 80%. Já a probabilidade
de acertar uma determinada faixa do alvo é igual a razão entre a área dessa faixa e a área total do alvo. Sendo assim, a
probabilidade de ele acertar uma das faixas brancas do alvo é igual a
Henrique começou a praticar tiro esportivo e treina em um alvo circular com 40 centímetros de diâmetro máximo, com 10 círculos concêntricos, ou seja, de mesmo centro, cujos raios podem ser identificados na ilustração que segue.

Considerando que Henrique ainda é um amador no esporte, a probabilidade de ele acertar o alvo é de 80%. Já a probabilidade
de acertar uma determinada faixa do alvo é igual a razão entre a área dessa faixa e a área total do alvo. Sendo assim, a
probabilidade de ele acertar uma das faixas brancas do alvo é igual a
O maior volume de uma pizza no formato circular que o proprietário pode fabricar para
caber nessa embalagem corresponde a, aproximadamente:
(Aproxime os resultados para o centésimo)
Uma rede de pizzaria utiliza embalagens de papelão para fazer suas entregas em domicílio, como o modelo da figura a seguir. Na hora de comprar as embalagens pela internet, o proprietário observou que a maior embalagem correspondia a um prisma octogonal regular de altura 5 cm e com aresta da base medindo 35 cm.
Considere: sen (22,5)° = 0,383, cos (22,5)° = 0,924, tg (22,5)°= 0,414 e π = 3,14.

Imagem disponível em: < http://produto.mercadolivre.com.br/MLB-749342112-caixa-de-pizza-caixa-de-papelopizzas-pizzaria-35cm-_JM> Acesso em: 30 abr 2017.
28 052,02 cm3
9 350 cm3
1 327,28 cm3
663,64 cm3
324 cm3
O volume da embalagem equivale a aproximadamente:
O volume da embalagem equivale a aproximadamente:
Uma rede de pizzaria utiliza embalagens de papelão para fazer suas entregas em domicílio, como o modelo da figura a seguir. Na hora de comprar as embalagens pela internet, o proprietário observou que a maior embalagem correspondia a um prisma octogonal regular de altura 5 cm e com aresta da base medindo 35 cm.
Considere: sen (22,5)° = 0,383, cos (22,5)° = 0,924, tg (22,5)°= 0,414 e π = 3,14.

Imagem disponível em: < http://produto.mercadolivre.com.br/MLB-749342112-caixa-de-pizza-caixa-de-papelopizzas-pizzaria-35cm-_JM> Acesso em: 30 abr 2017.
Um triângulo isósceles tem a base medindo 10 e um dos
ângulos da base medindo 45°. A medida do raio da
circunferência inscrita nesse triângulo é:
Considere, na Figura 2, o quadrado ABCD inscrito na circunferência de equação x2 + y2 -6x -10y 25 = 0 e o quadrado EFGH circunscrito à circunferência de equação x2 + y2 -4x - 10y + 4 = 0.
 Figura 2: Quadrados
Figura 2: Quadrados
Com base nas informações e na Figura 2, analise as sentenças.
I. A diferença das áreas dos quadrados EFGH e ABCD é de 82 unidades de área.
II. Se os lados do quadrado EFGH forem paralelos aos eixos do plano cartesiano e às diagonais do quadrado ABCD, então a área do triângulo EAB é de 12 unidades de área.
III. A soma dos perímetros dos quadrados ABCD e EFGH é de 52√2 unidades de comprimento.
Assinale a alternativa correta.

Brazuca, a bola oficial da Copa do Mundo de 2014, quando completamente cheia, pode ser considerada perfeitamente esférica
e possui circunferência máxima de 68 cm.
Nessas condições, podemos afirmar corretamente que a medida do raio da Brazuca mais se aproxima, em centímetros, de
Considere dois círculos concêntricos em um
ponto O e de raios distintos; dois segmentos
de reta  perpendiculares em O,
como na figura abaixo.
perpendiculares em O,
como na figura abaixo.

Sabendo que o ângulo  mede 30° e que
o segmento
mede 30° e que
o segmento  mede 12, pode-se afirmar
que os diâmetros dos círculos medem
mede 12, pode-se afirmar
que os diâmetros dos círculos medem
Considere dois círculos concêntricos em um
ponto O e de raios distintos; dois segmentos
de reta  perpendiculares em O,
como na figura abaixo.
perpendiculares em O,
como na figura abaixo.

Sabendo que o ângulo  mede 30° e que
o segmento
mede 30° e que
o segmento  mede 12, pode-se afirmar
que os diâmetros dos círculos medem
mede 12, pode-se afirmar
que os diâmetros dos círculos medem
Num projeto hidráulico, um cano com diâmetro externo de 6 cm será
encaixado no vão triangular de uma superfície, como ilustra a figura
ao lado. Que porção x da altura do cano permanecerá acima da
superfície?


Na Figura 2 sem escala, o raio da circunferência de centro
O
é
r = 3cm
e o segmento 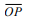 mede
5cm.
mede
5cm.

Sabendo que o segmento 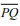 tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento
tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento 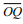 mede:
mede:
Na Figura 2 sem escala, o raio da circunferência de centro
O
é
r = 3cm
e o segmento 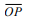 mede
5cm.
mede
5cm.

Sabendo que o segmento 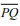 tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento
tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento 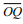 mede:
mede:


A equação x2
+ y2
– 10x + 6y + 30 = 0 representa uma circunferência de centro C(a,b) e raio r. Nessas
condições, o valor de (a + b + r) é
Uma partícula em movimento descreve sua trajetória sobre semicircunferências traçadas a partir de um ponto P0
, localizado
em uma reta horizontal r, com deslocamento sempre no sentido
horário. A figura mostra a trajetória da partícula, até o ponto P3
,
em r. Na figura, O, O1
e O2
são os centros das três primeiras
semicircunferências traçadas e R, R/2 e R/4 seus respectivos
raios.

A trajetória resultante do movimento da partícula será obtida repetindo-se esse comportamento indefinidamente, sendo o centro e o
raio da n-ésima semicircunferência dados por On e Rn = R/2n ,
respectivamente, até o ponto Pn
, também em r. Nessas condições,
o comprimento da trajetória descrita pela partícula, em função do
raio R, quando n tender ao infinito, será igual a

Seja Z um número complexo cujo afixo P está localizado no
1º
quadrante do plano complexo, e sejam I, II, III, IV e V os
afixos de cinco outros números complexos, conforme indica
a figura seguinte.
Se a circunferência traçada na figura possui raio 1 e está centrada na origem do plano complexo, então o afixo de 1/Z pode
ser
