Questõesde UDESC sobre Aritmética e Problemas
Duas engrenagens X e Y têm 22 e 34 dentes, respectivamente. Elas estão encaixadas de
modo que um motor ligado à engrenagem X a faz girar no sentido anti-horário e essa faz a
engrenagem Y girar no sentido horário. Sabe-se que a engrenagem Y demora 2 minutos para
realizar uma revolução completa. As duas engrenagens retornarão à posição inicial após:
Operando a soma de frações abaixo e simplificando a expressão 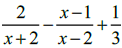 , obtém-se:
, obtém-se:
Operando a soma de frações abaixo e simplificando a expressão 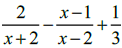 , obtém-se:
, obtém-se:





Cristiane ligou para o delivery de uma pizzaria e pediu uma pizza média, cujo diâmetro é de 30
cm. Porém, a pizzaria estava sem embalagens disponíveis para entregar a pizza média e
propôs que Cristiane levasse duas pizzas pequenas, cada uma com raio de 10 cm, pelo
mesmo valor de uma pizza média. Ao aceitar a proposta da pizzaria, e desconsiderando a
espessura das pizzas, é correto afirmar que Cristiane recebeu:
Cláudio e João, após jogarem 25 partidas de xadrez, apresentavam o placar de 14 vitórias de
Cláudio contra 10 vitórias de João. João decidiu melhorar seu desempenho e seu objetivo é
ganhar todas as próximas partidas até que sua taxa percentual de vitórias aumente em pelo
menos 12%. O número mínimo de vitórias consecutivas para que o objetivo de João seja
alcançado é igual a:
João precisará percorrer um trajeto de 200 km. O limite de velocidade em um trecho de 55 km
é de 110 km/h; para 85 km do percurso o limite é de 100 km/h, e no restante do trajeto o limite
é de 80 km/h. Se João andar exatamente no limite da pista em cada trecho e não fizer
nenhuma parada, o tempo que ele levará para percorrer todo o trajeto é de:
Uma empresa, hoje, atua com um quadro de 16 funcionários em uma jornada diária de 6 horas.
Nessas condições, ela é capaz de produzir 120 produtos por dia. O número de funcionários
necessários para produzir 200 produtos, caso a jornada de trabalho seja aumentada para 8
horas diárias, será de:


Roberto decidiu presentear sua namorada com um anel. Como não conhecia o diâmetro exato
que deveria ter o anel, ele teve a ideia de ver qual seria o diâmetro de um anel adequado para
ele, e comprar um com a medida de diâmetro 10% menor para sua namorada. Uma vez feita a
medição, o que melhor se ajustou em seu dedo foi um anel de 20 milímetros de diâmetro.
Após dado o presente, constatou-se que a ideia de Roberto não foi bem sucedida, sendo
necessário ajustar o anel para que ele coubesse adequadamente no dedo da namorada. Para
isso foram retirados 0,65 cm do comprimento do anel. Após o ajuste, a medida do raio do anel,
em milímetros, ficou aproximadamente igual a:


Uma loja de roupas resolveu fazer a seguinte promoção: comprando camisetas de mesmo
valor, a segunda terá um desconto de 20% em relação à primeira, e a terceira 50% de
desconto em relação ao valor pago na segunda. Se o valor total pago foi de R$ 286,00, então o
preço pago na compra de apenas uma camiseta é de:


A Figura 1 ilustra duas moedas brasileiras, a
de R$ 1,00 e a de R$ 0,50, descritas abaixo.

Figura 1: Moedas brasileiras
Moeda de R$ 1,00 – As faces da moeda são
compostas por dois círculos concêntricos. O
diâmetro do círculo maior é igual a 2,8 cm e o
diâmetro do círculo menor é igual a 1,8 cm. A
espessura desta moeda é igual a 1,5 mm.
Moeda de R$ 0,50 – As faces da moeda são
compostas por um círculo de diâmetro igual a
2,2 cm. A espessura desta moeda é igual a 3 mm.
Com base nestas informações, analise as
proposições abaixo.
I. O volume de metal necessário para cunhar
a região situada entre os círculos
concêntricos da moeda de R$ 1,00 é
aproximadamente 0,1725 π cm3
.
II. Para cunhar uma moeda de R$ 1,00 é
necessário aproximadamente 0,069 π cm3
de metal a mais que para cunhar uma
moeda de R$ 0,50.
III. A área entre os círculos concêntricos da
moeda de R$ 1,00 é 0,34 π cm2 maior que
a do círculo interno.
Assinale a alternativa correta.
A Figura 1 ilustra duas moedas brasileiras, a de R$ 1,00 e a de R$ 0,50, descritas abaixo.

Figura 1: Moedas brasileiras
Suponha que o valor do quilowatt hora (kWh)
varie de acordo com a Tabela 1 e que, ao valor
pago à Companhia de Energia Elétrica pela
quantidade de kWh consumido, devem ser
acrescentados ainda os tributos apresentados
na Tabela 2.
Tabela 1: Tarifa (R$/kWh) Quantidade de kWh Tarifa (R$/kWh) De 0 a 150 0,36 A partir de 150 0,42
Tabela 2: TributosTributos Quantidade de kWh %ICMS De 0 a 150 12 A partir de 150 25PIS/PASEP 1COFINS 4
Com base nas informações acima, é correto
afirmar que a fatura de energia elétrica de uma
unidade residencial que consome em média
175 kWh por mês apresente valor entre:
Dois amigos viajaram juntos por um período
de sete dias. Durante esse tempo, um deles
pronunciou, precisamente, 362.880 palavras. A
fim de saber se falara demais, ele se questionou
sobre quantas palavras enunciara por minuto.
Considerando que ele dormiu oito horas diárias,
o número médio de palavras ditas por minuto
foi:
A soma de todos os números naturais múltiplos de 9 que são formados por quatro algarismos
deixa como resto:
Uma loja de material para pintura fabrica tintas de cores personalizadas, usando uma máquina que mistura até
3 cores iniciais em proporções que podem ser ajustadas de 20% em 20%. Sabendo que há 4 cores iniciais para
se escolher, o número de cores que podem ser oferecidas, incluindo as iniciais puras, é:
Ana tem uma impressora 3D que utiliza o polímero PLA (poliácido láctico) para imprimir objetos. Ela comprou
1 quilograma de PLA em formato de fio cilíndrico com diâmetro de 1,75 milímetro, no valor de R$120,00. Para
imprimir um objeto A, o programa de impressão estima gastar 12 metros do material. Sabendo que cada metro
de PLA tem 3 gramas, o valor gasto em filamento para imprimir esse objeto é:
Uma pirâmide regular de base hexagonal tem o vértice sobre uma semiesfera e a base inscrita na base desta
semiesfera. Sabendo que a aresta lateral dessa pirâmide mede 10 cm, então o volume é igual a:
A Tabela 1 representa a tabela nutricional de um determinado tablete de chocolate de 100 g.
Tabela 1 – Informação Nutricional: Porção 1/4 do tablete

A empresa que produz este chocolate pretende reduzir o tamanho do tablete de 100g para 85g
e, para isto, precisará atualizar os valores da Tabela nutricional. Além disso, será incluída uma
nova coluna, que conterá os valores diários percentuais de ingestão (VD%) referentes a cada
item, com base em uma dieta de 2000 Kcal, de acordo com a Tabela 2.
Tabela 2 - Valores diários de referência de nutrientes

Após a atualização da Tabela 1, o percentual do recomendado diário de carboidratos ingeridos
em uma porção do novo tablete será equivalente a:
A Tabela 1 representa a tabela nutricional de um determinado tablete de chocolate de 100 g.
Tabela 1 – Informação Nutricional: Porção 1/4 do tablete

A empresa que produz este chocolate pretende reduzir o tamanho do tablete de 100g para 85g e, para isto, precisará atualizar os valores da Tabela nutricional. Além disso, será incluída uma nova coluna, que conterá os valores diários percentuais de ingestão (VD%) referentes a cada item, com base em uma dieta de 2000 Kcal, de acordo com a Tabela 2.
Tabela 2 - Valores diários de referência de nutrientes

Após a atualização da Tabela 1, o percentual do recomendado diário de carboidratos ingeridos
em uma porção do novo tablete será equivalente a:


Em 1958, como trote para os calouros da universidade de Harvard, nos Estados Unidos, um
grupo de estudantes precisou medir o comprimento da ponte de Harvard (entre Boston e
Cambridge, em Massachusetts), usando como padrão de medida um dos próprios estudantes,
um rapaz chamado Oliver R. Smoot. Após horas de medição, com o estudante deitando-se no
chão e levantando-se sucessivas vezes para as medidas, concluiu-se que a ponte tinha 364,4
smoots, +/- 1 orelha.
A brincadeira fez tanto sucesso e a medição tornou-se tão popular que, na década de 1980, a
ponte foi reformada pela prefeitura, que encomendou blocos de concreto personalizados de 1
smoot de comprimento para a reforma, eternizando as marcações colocadas no solo, que hoje
já constam até no sistema de conversão de medidas da ferramenta Google.
Ainda mais interessante é o fato de que, alguns anos após formado, Oliver Smoot tornou-se
diretor da ANSI, o Instituto Nacional Americano de Padrões (“American National Standards
Institute”) e depois presidente da ISO, a Organização Internacional para Padronização
(“International Organization for Standardization”).
Sabendo que Oliver Smoot tinha 5 pés e 7 polegadas de altura na ocasião da medida,
desprezando o erro de +/- 1 orelha, e assumindo 1 pé = 30,5 cm e 1 polegada = 2,5 cm, o
comprimento da ponte é:


De forma simplificada, a umidade relativa do ar é calculada pela relação entre a quantidade de
vapor de água presente no ar e a quantidade máxima desse vapor no ar, antes que ele fique
saturado e a água comece a condensar para a forma líquida, para condições específicas de
temperatura e de pressão.
Um ambiente fechado de 40 m3 apresenta inicialmente 100% de umidade relativa do ar, com
20 g de vapor de água por metro cúbico. Se for colocado neste ambiente um condicionador de
ar, que retira do ambiente 1 kg de água por hora (de forma constante), e um umidificador, que
adiciona 600 g de água por hora (de forma constante), e são ligados simultaneamente, logo a
umidade relativa nesse ambiente, após 30 minutos, será de:


Desde 2007 a Receita Federal tem alterado as bases de cálculo para a declaração do imposto de renda de pessoas físicas, aumentando o intervalo das faixas salariais e da parcela a ser deduzida no cálculo do imposto. Além disso, desde 2009 também foram adotadas duas novas alíquotas, de 7,5% e 22,5%, juntamente com as de 15% e 27,5% já existentes. As tabelas 1 e 2 evidenciam estas mudanças, mostrando as faixas do imposto de renda de pessoa física, conforme o nível salarial do contribuinte, para os exercícios de 2009 (ano-calendário de 2008) e de 2010 (ano- calendário de 2009), respectivamente.

Um contribuinte sabe que, para calcular o quanto de imposto de renda irá pagar mensalmente, deve multiplicar o valor do seu salário mensal pela alíquota correspondente e descontar desse total a respectiva parcela a ser deduzida. Suponha que o salário mensal deste contribuinte tenha permanecido inalterado durante os anos de 2008 e 2009 e que, no exercício de 2009, ele pagou 109,08 reais mensais de imposto de renda. Então, para o exercício de 2010, este mesmo contribuinte irá pagar:

Um contribuinte sabe que, para calcular o quanto de imposto de renda irá pagar mensalmente, deve multiplicar o valor do seu salário mensal pela alíquota correspondente e descontar desse total a respectiva parcela a ser deduzida. Suponha que o salário mensal deste contribuinte tenha permanecido inalterado durante os anos de 2008 e 2009 e que, no exercício de 2009, ele pagou 109,08 reais mensais de imposto de renda. Então, para o exercício de 2010, este mesmo contribuinte irá pagar: