00349182-e1
UCPEL 2005 - Matemática - Análise Combinatória em Matemática
Na compra de um certo número de caixas de
pêssegos, um feirante pagou R$ 360,00. Na semana
seguinte, o preço aumentou R$ 24,00, por caixa. Com
a mesma quantia, o feirante comprou 4 caixas a
menos. Então, o número de caixas que ele comprou é:
Na compra de um certo número de caixas de
pêssegos, um feirante pagou R$ 360,00. Na semana
seguinte, o preço aumentou R$ 24,00, por caixa. Com
a mesma quantia, o feirante comprou 4 caixas a
menos. Então, o número de caixas que ele comprou é:
A
10
B
12
C
15
D
18
E
6
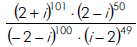 obtém-se:
obtém-se:
