Um computador atribui um número inteiro
diferente a cada caractere do teclado. Para transmitir
uma mensagem pela internet, esta é transformada em
uma sequência de números inteiros consecutivos que
é codificada do seguinte modo: A cada grupo de 4
caracteres consecutivos a, b, c, d, o computador
multiplica a matriz  à direita pela matriz
à direita pela matriz  e
transmite o resultado
e
transmite o resultado  na sequência x, y, v, w.
Por exemplo, a sequência 1, 8, 11, 3 é transmitida
como a sequência 10, 19, 25, 39. Então,
na sequência x, y, v, w.
Por exemplo, a sequência 1, 8, 11, 3 é transmitida
como a sequência 10, 19, 25, 39. Então,
 à direita pela matriz
à direita pela matriz  e
transmite o resultado
e
transmite o resultado  na sequência x, y, v, w.
Por exemplo, a sequência 1, 8, 11, 3 é transmitida
como a sequência 10, 19, 25, 39. Então,
na sequência x, y, v, w.
Por exemplo, a sequência 1, 8, 11, 3 é transmitida
como a sequência 10, 19, 25, 39. Então,











 um sistema de equações nas incógnitas x e y. Os valores de k para que a solução
gráfica desse sistema pertença ao interior do terceiro quadrante do plano cartesiano são dados pelo intervalo
um sistema de equações nas incógnitas x e y. Os valores de k para que a solução
gráfica desse sistema pertença ao interior do terceiro quadrante do plano cartesiano são dados pelo intervalo for maior do que zero, então
for maior do que zero, então  Assinale a alternativa correta:
Assinale a alternativa correta:  , em que
, em que 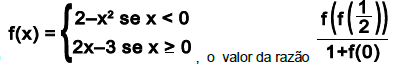 é igual a
é igual a
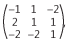 , B =
, B = 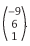 e C =
e C = 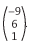 .
.


