Na figura abaixo, um corpo de massa M
desliza com velocidade constante sobre um
plano inclinado que forma um ângulo θ com o
plano horizontal.
Considere g o módulo da aceleração da
gravidade e despreze a resistência do ar.

Assinale a alternativa que preenche
corretamente as lacunas do enunciado abaixo,
na ordem em que aparecem.
Quando o centro de massa do corpo desce
uma altura h, os trabalhos realizados pela
força peso e pela força de atrito entre corpo e
plano são, respectivamente, ........ e ........ .
Na figura abaixo, um corpo de massa M desliza com velocidade constante sobre um plano inclinado que forma um ângulo θ com o plano horizontal.
Considere g o módulo da aceleração da gravidade e despreze a resistência do ar.

Assinale a alternativa que preenche corretamente as lacunas do enunciado abaixo, na ordem em que aparecem.
Quando o centro de massa do corpo desce
uma altura h, os trabalhos realizados pela
força peso e pela força de atrito entre corpo e
plano são, respectivamente, ........ e ........ .
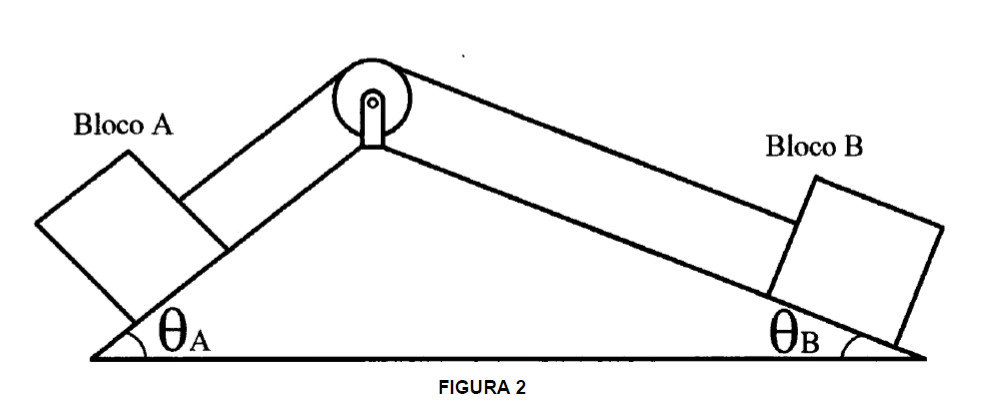








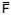 , sendo aplicada à caixa paralelamente
à superfície inclinada, como mostra a figura 2.
, sendo aplicada à caixa paralelamente
à superfície inclinada, como mostra a figura 2.
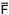 é 200 N. Se o ângulo
for aumentado para um valor θ
é 200 N. Se o ângulo
for aumentado para um valor θ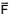 passa
a ser de
passa
a ser de





 os coeficientes de atrito estático e cinético, respectivamente, entre o bloco e a superfície inclinada do plano; “a" a aceleração e “v" a velocidade do bloco; “g" o valor da aceleração local da gravidade:
os coeficientes de atrito estático e cinético, respectivamente, entre o bloco e a superfície inclinada do plano; “a" a aceleração e “v" a velocidade do bloco; “g" o valor da aceleração local da gravidade:

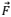 formando um ângulo
formando um ângulo 