Questõessobre Movimento Harmônico
Considere duas situações em que dois pêndulos (A e B) de mesmo comprimento oscilam
livremente em um cenário isento de resistência do ar. A esfera A tem o mesmo volume que a B,
todavia, por serem de materiais diferentes, a densidade de A é um terço da de B. Ambas são
soltas da mesma altura e do repouso para iniciarem a oscilação.

Com base na situação descrita, são feitas algumas afirmações.
I) O período de oscilação de A é igual ao de B.
II) A velocidade com que B passa pelo ponto mais baixo da trajetória é três vezes maior do que a
velocidade com que A passa pelo mesmo ponto.
III) A aceleração com que B passa pelo ponto mais baixo da trajetória é maior do que a de A nesse
mesmo ponto.
Em relação às afirmações acima, marque V para as verdadeiras e F para as falsas e assinale
a alternativa correta.
Considere duas situações em que dois pêndulos (A e B) de mesmo comprimento oscilam livremente em um cenário isento de resistência do ar. A esfera A tem o mesmo volume que a B, todavia, por serem de materiais diferentes, a densidade de A é um terço da de B. Ambas são soltas da mesma altura e do repouso para iniciarem a oscilação.

Com base na situação descrita, são feitas algumas afirmações.
I) O período de oscilação de A é igual ao de B.
II) A velocidade com que B passa pelo ponto mais baixo da trajetória é três vezes maior do que a velocidade com que A passa pelo mesmo ponto.
III) A aceleração com que B passa pelo ponto mais baixo da trajetória é maior do que a de A nesse mesmo ponto.
Em relação às afirmações acima, marque V para as verdadeiras e F para as falsas e assinale
a alternativa correta.
Considere uma massa (m) pendurada por uma mola inextensível com constante elástica (k), em um local
de gravidade g e forças dissipativas nulas.

É CORRETO afirmar que

Um corpo oscila com movimento harmônico simples. Sua posição, com o tempo, varia conforme a equação x (t) = 0,30 cos (2π t + π) onde x está em metros, t em segundos e a fase está em radianos. Assim, a frequência, o período e a frequência angular são, respectivamente,
Observe o poema visual de E. M. de Melo e Castro.

Suponha que o poema representa as posições de um pêndulo
simples em movimento, dadas pelas sequências de letras
iguais. Na linha em que está escrita a palavra pêndulo, indicada
pelo traço vermelho, cada letra corresponde a uma localização
da massa do pêndulo durante a oscilação, e a letra
P indica a posição mais baixa do movimento, tomada como
ponto de referência da energia potencial. Considerando as
letras da linha da palavra pêndulo, é correto afirmar que
Observe o poema visual de E. M. de Melo e Castro.

Suponha que o poema representa as posições de um pêndulo
simples em movimento, dadas pelas sequências de letras
iguais. Na linha em que está escrita a palavra pêndulo, indicada
pelo traço vermelho, cada letra corresponde a uma localização
da massa do pêndulo durante a oscilação, e a letra
P indica a posição mais baixa do movimento, tomada como
ponto de referência da energia potencial. Considerando as
letras da linha da palavra pêndulo, é correto afirmar que
Considere um pêndulo de relógio de parede
feito com um fio flexível, inextensível, de massa
desprezível e com comprimento de 24,8 cm. Esse fio
prende uma massa puntiforme e oscila com uma
frequência próxima a 1 Hz. Considerando que a
força de resistência do ar seja proporcional à
velocidade dessa massa, é correto afirmar que
Em um parque de diversões, existe uma atração na qual o
participante tenta acertar bolas de borracha na boca da figura
de um palhaço que, presa a uma mola ideal, oscila em movimento
harmônico simples entre os pontos extremos A e E,
passando por B, C e D, de modo que em C, ponto médio do
segmento AE, a mola apresenta seu comprimento natural,
sem deformação.

Uma pessoa, ao fazer suas tentativas, acertou a primeira
bola quando a boca passou por uma posição em que o módulo de sua aceleração é máximo e acertou a segunda bola
quando a boca passou por uma posição onde o módulo de
sua velocidade é máximo. Dos pontos indicados na figura,
essas duas bolas podem ter acertado a boca da figura do
palhaço, respectivamente, nos pontos
Em um parque de diversões, existe uma atração na qual o participante tenta acertar bolas de borracha na boca da figura de um palhaço que, presa a uma mola ideal, oscila em movimento harmônico simples entre os pontos extremos A e E, passando por B, C e D, de modo que em C, ponto médio do segmento AE, a mola apresenta seu comprimento natural, sem deformação.

Uma pessoa, ao fazer suas tentativas, acertou a primeira
bola quando a boca passou por uma posição em que o módulo de sua aceleração é máximo e acertou a segunda bola
quando a boca passou por uma posição onde o módulo de
sua velocidade é máximo. Dos pontos indicados na figura,
essas duas bolas podem ter acertado a boca da figura do
palhaço, respectivamente, nos pontos
Um pêndulo simples, constituído por um fio de comprimento e uma pequena esfera, é colocado em oscilação. Uma haste horizontal rígida é inserida perpendicularmente ao plano de oscilação desse pêndulo, interceptando o movimento do fio na metade do seu comprimento, quando ele está na direção vertical. A partir desse momento, o período do movimento da esfera é dado por





Na geração da voz humana, a garganta e a cavidade oral agem
como um tubo, com uma extremidade aproximadamente fechada
na base da laringe, onde estão as cordas vocais, e uma
extremidade aberta na boca. Nessas condições, sons são emitidos
com maior intensidade nas frequências e comprimentos
de ondas para as quais há um nó (N) na extremidade fechada e
um ventre (V) na extremidade aberta, como ilustra a figura. As
frequências geradas são chamadas harmônicos ou modos normais
de vibração. Em um adulto, este tubo do trato vocal tem
aproximadamente 17 cm. A voz normal de um adulto ocorre
em frequências situadas aproximadamente entre o primeiro e
o terceiro harmônicos.

Considerando que a velocidade do som no ar é 340 m/s, os
valores aproximados, em hertz, das frequências dos três primeiros
harmônicos da voz normal de um adulto são

Considerando que a velocidade do som no ar é 340 m/s, os valores aproximados, em hertz, das frequências dos três primeiros harmônicos da voz normal de um adulto são
Para efeito de cálculos, considere π =3 e g = 10 m /s².
Para que não ocorra deslizamento entre os blocos por conta do movimento harmônico simples (MHS), o coeficiente de atrito estático entre as superfícies desses blocos é igual a:
Para que não ocorra deslizamento entre os blocos por conta do movimento harmônico simples (MHS), o coeficiente de atrito estático entre as superfícies desses blocos é igual a:

Uma massa m, presa a um ponto fixo por meio de uma mola de massa desprezível e constante elástica K, oscila sem atrito em um movimento unidimensional. Em um dado sistema de referência, a posição x da massa pode ser dada por x = xmáxsen(ωt), com ω2 =K/m, e a velocidade por v = ωxmáxcos (ωt). Neste caso, a energia mecânica total do sistema massa-mola é
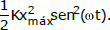
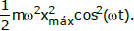
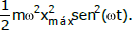
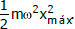
Sabendo-se que uma onda eletromagnética se propaga em um meio com velocidade igual à metade da velocidade da luz e tem a forma descrita pela equação: A cos(wt + Ø)
Onde:
Tempo: t
Amplitude: A
Frequência angular: w
Defasagem angular da onda: Ø
Velocidade da luz no vácuo: c
As expressões CORRETAS para o período T e o comprimento de onda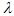 são, respectivamente:
são, respectivamente:
Onde:
Tempo: t
Amplitude: A
Frequência angular: w
Defasagem angular da onda: Ø
Velocidade da luz no vácuo: c
As expressões CORRETAS para o período T e o comprimento de onda
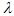 são, respectivamente:
são, respectivamente:Conecta-se à placa positiva de um capacitor de placas paralelas um fio isolante inextensível, de comprimento L e massa desprezível, que tem preso à sua extremidade uma bolinha de massa m e carga +q , conforme ilustra a figura.

Sendo E o módulo do campo elétrico entre as placas e desprezando a resistência do ar, o período de pequenas oscilações desse pêndulo é:

Sendo E o módulo do campo elétrico entre as placas e desprezando a resistência do ar, o período de pequenas oscilações desse pêndulo é:

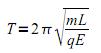



Nos dois itens a seguir, que são do tipo B, faça o que se pede, desconsiderando, para as marcações na folha de respostas, a parte fracionária do resultado final obtido, após realizar todos os cálculos solicitados.
Considere que um corpo em oscilação livre com período T esteja preso a um teto por um fio submetido a uma temperatura de 0 °C. Considere ainda que, quando submetido a uma temperatura e 1.000 °C, esse corpo, preso ao teto pelo mesmo fio, oscila livremente com período  . Nessa situação, sabendo que o coeficiente de dilatação linear do fio é igual a 2,1 × 10 -4 °C -1 calcule
. Nessa situação, sabendo que o coeficiente de dilatação linear do fio é igual a 2,1 × 10 -4 °C -1 calcule 
( a resposta é 011 )
Considere que um corpo em oscilação livre com período T esteja preso a um teto por um fio submetido a uma temperatura de 0 °C. Considere ainda que, quando submetido a uma temperatura e 1.000 °C, esse corpo, preso ao teto pelo mesmo fio, oscila livremente com período
 . Nessa situação, sabendo que o coeficiente de dilatação linear do fio é igual a 2,1 × 10 -4 °C -1 calcule
. Nessa situação, sabendo que o coeficiente de dilatação linear do fio é igual a 2,1 × 10 -4 °C -1 calcule 
( a resposta é 011 )
O pistão é ligado, por meio da haste BC, a um disco que gira em torno do centro A. Considere que:
• o raio AB e a haste BC medem, respectivamente, 1 polegada e 4 polegadas;
• à medida que o disco gira, o pistão move-se verticalmente para cima ou para baixo, variando a distância AC e o ângulo BÂC.
Se a medida do ângulo BÂC é dada por x radianos, a distância entre A e C, em polegadas, pode ser obtida pela seguinte equação
• o raio AB e a haste BC medem, respectivamente, 1 polegada e 4 polegadas;
• à medida que o disco gira, o pistão move-se verticalmente para cima ou para baixo, variando a distância AC e o ângulo BÂC.
Se a medida do ângulo BÂC é dada por x radianos, a distância entre A e C, em polegadas, pode ser obtida pela seguinte equação

Se, para t = 5 s, o jovem passa pela primeira vez na posição  , então, o período de oscilação T é inferior a 8 s.
, então, o período de oscilação T é inferior a 8 s.
 , então, o período de oscilação T é inferior a 8 s.
, então, o período de oscilação T é inferior a 8 s.

De acordo com o primeiro modelo, um movimento completo de ida e volta do joão-bobo ocorre em 2 s.

Tendo como referência essas informações, julgue os itens de 72 a 83 e faça o que se pede no item 84, que é do tipo C, e no item 85, que é do tipo B.
Em t = log2(40) s, a amplitude de movimento instantâneo do joão-bobo, de acordo com o segundo modelo, é igual a um décimo da amplitude de acordo com o primeiro modelo.

Tendo como referência essas informações, julgue os itens de 72 a 83 e faça o que se pede no item 84, que é do tipo C, e no item 85, que é do tipo B.
Ambos os modelos descrevem funções periódicas.

Tendo como referência essas informações, julgue os itens de 72 a 83 e faça o que se pede no item 84, que é do tipo C, e no item 85, que é do tipo B.