Questõessobre Lançamento Oblíquo

InícioTodas as questões
1
1
Foram encontradas 64 questões
c82178a6-e3
FAG 2014 - Física - Cinemática, Lançamento Oblíquo

Um menino deseja saltar do topo de um barranco de 5,0m de altura para cair na parte mais funda de um poço de água cristalina e calma.



Adotando g = 10m/s2 e considerando os dados da figura, a velocidade horizontal adequada para que o menino consiga o seu intento é, em m/s.

A
1,0
B
2,5
C
4,0
D
5,0
E
7,0
65fcc143-e3
UEM 2013, UEM 2013, UEM 2013 - Física - Cinemática, Lançamento Oblíquo

Supondo que, para fazer um salto em distância, Bolt mantém a velocidade em módulo, porém mudando a direção da velocidade para 45° com a direção horizontal, então ele saltaria uma distância maior do que 20,0 m .

FÍSICA – Formulário e Constantes

Na prova dos 100 metros rasos, o atleta Usain Bolt consegue atingir uma velocidade máxima de v = 12,4m/s. Considerando essa velocidade e a aceleração da gravidade g =10,0 m/s2, assinale o que for correto. 
C
Certo
E
Errado
2f90fd0b-e5
UFCG 2009, UFCG 2009 - Física - Cinemática, Lançamento Oblíquo

A invasão francesa do Rio de Janeiro em 1711 demonstrou a precariedade da defesa da Baía da Guanabara baseada em uso de canhões. A eficiência dessas armas era muito limitada e questionada:


Um experimento sobre a eficiência das bocas de fogo, em tiros de longo alcance, feito em 1729 pelo engenheiro militar português Manoel de Azevedo Fortes (1660 — 1749), levou-o a concluir: “Com armas de fogo se atira longe, e sem pontaria certa; e assim a maior parte das balas não faz efeito algum.” Outro engenheiro militar do mesmo período, José Fernandes Pinto Alpoim (1700 — 1765), confirmava a opinião de Fortes, afirmando que a imprevisibilidade tornava sem utilidade as tabelas de alcance usadas então pelos artilheiros.


MARTINS, Ricardo Vieira. A invasão francesa em 1711 e o despreparo da artilharia portuguesa. Ciência Hoje, v.43, n.257, mar.2009, p.35.


As dificuldades apontadas pelos engenheiros militares do século XVIII podem estar relacionadas, EXCETO, com

A
a atuação da resistência do ar sobre o alcance do projétil.
B
a relação entre o alcance e o peso do projétil.
C
o fato de que apenas mantida a inclinação do canhão e o poder de fogo, não se pode garantir a precisão das tabelas de alcance em quaisquer condições de tiro.
D
as variações da aceleração do projétil.
E
o fato de o alcance, independentemente da presença do ar, ser sempre o máximo possível para a inclinação do canhão igual a 45º.
f0574da9-e0
UEM 2010 - Física - Cinemática, Lançamento Oblíquo

Uma partícula de massa m é lançada obliquamente para cima, próxima à superfície da Terra, com uma velocidade v. Quando atinge o ponto mais alto de sua trajetória, a partícula está a uma altura H em relação ao solo. Desprezando a resistência do ar e considerando que g é o módulo da aceleração da gravidade, é correto afirmar que, quando a partícula atinge a altura H,

o módulo do vetor velocidade da partícula é zero.

FÍSICA - Formulário e Constantes Físicas
C
Certo
E
Errado
f04c3a07-e0
UEM 2010 - Física - Dinâmica, Cinemática, Trabalho e Energia, Lançamento Oblíquo

Uma partícula de massa m é lançada obliquamente para cima, próxima à superfície da Terra, com uma velocidade v. Quando atinge o ponto mais alto de sua trajetória, a partícula está a uma altura H em relação ao solo. Desprezando a resistência do ar e considerando que g é o módulo da aceleração da gravidade, é correto afirmar que, quando a partícula atinge a altura H,

o trabalho W realizado pela força peso sobre a partícula é W = - mgH.

FÍSICA - Formulário e Constantes Físicas
C
Certo
E
Errado
f0530f91-e0
UEM 2010 - Física - Dinâmica, Cinemática, Trabalho e Energia, Lançamento Oblíquo

Uma partícula de massa m é lançada obliquamente para cima, próxima à superfície da Terra, com uma velocidade v. Quando atinge o ponto mais alto de sua trajetória, a partícula está a uma altura H em relação ao solo. Desprezando a resistência do ar e considerando que g é o módulo da aceleração da gravidade, é correto afirmar que, quando a partícula atinge a altura H,

a variação da energia cinética ∆Ec da partícula é ∆Ec = - mgH.

FÍSICA - Formulário e Constantes Físicas
C
Certo
E
Errado
f04f69cc-e0
UEM 2010 - Física - Dinâmica, Cinemática, Trabalho e Energia, Lançamento Oblíquo

Uma partícula de massa m é lançada obliquamente para cima, próxima à superfície da Terra, com uma velocidade v. Quando atinge o ponto mais alto de sua trajetória, a partícula está a uma altura H em relação ao solo. Desprezando a resistência do ar e considerando que g é o módulo da aceleração da gravidade, é correto afirmar que, quando a partícula atinge a altura H,

a variação da energia potencial ∆Ep da partícula é ∆Ep = mgH

FÍSICA - Formulário e Constantes Físicas
C
Certo
E
Errado
f048ee05-e0
UEM 2010 - Física - Dinâmica, Cinemática, Trabalho e Energia, Impulso e Quantidade de Movimento, Lançamento Oblíquo

Uma partícula de massa m é lançada obliquamente para cima, próxima à superfície da Terra, com uma velocidade v. Quando atinge o ponto mais alto de sua trajetória, a partícula está a uma altura H em relação ao solo. Desprezando a resistência do ar e considerando que g é o módulo da aceleração da gravidade, é correto afirmar que, quando a partícula atinge a altura H,

o módulo da quantidade de movimento da partícula é igual a .

FÍSICA - Formulário e Constantes Físicas
C
Certo
E
Errado
773fb756-df
UEPB 2009 - Física - Cinemática, Lançamento Oblíquo



No dia 15 de junho de 2008, depois de um jogo sofrido, a seleção brasileira feminina de basquete conquistou a última vaga para os Jogos Olímpicos de Pequim, depois de vencerem as cubanas, numa partida repleta de adrenalina, na final da repescagem do Pré-Olímpico Mundial de Madri. Aos 4s finais do jogo, Mama fez um lançamento de bola, fechando o placar do jogo em 72 a 67. Considerando que, nesta última bola lançada pela jogadora em direção à cesta, a velocidade e trajetória da bola em um determinado instante são ilustradas pela figura ao lado, e que os efeitos do ar são desprezados, a(s) força(s) que age(m) sobre a bola, nesse instante, pode(m) ser representada(s) por:

A

B

C

D

E

e2c6d967-d9
UEPA 2009 - Física - Cinemática, Lançamento Oblíquo

As mulheres roubaram a cena na participação brasileira nos jogos Olímpicos de Pequim, na China. Foram delas dois dos três ouros que o país conquistou. No atletismo, no vôlei, no judô, na vela, no taekwondo e na ginástica artística, resultados inéditos. No salto em distância, Maurren Maggi conquistou a inédita medalha de ouro feminina numa competição individual, atingindo a marca de 7,04 metros.

Supondo que a massa da atleta esteja toda concentrada no seu centro de massa, sua trajetória poderá ser considerada parabólica, como ilustrado na figura, onde a atleta imprime uma velocidade vo, formando um ângulo α com a horizontal.



Desprezando a resistência do ar, é correto afirmar que a distância alcançada pela atleta:

A
É diretamente proporcional à aceleração da gravidade.
B

Depende da velocidade inicial do salto, vo.

C
É inversamente proporcional à velocidade inicial vo.
D
É diretamente proporcional à altura máxima atingida.
E
Independe do ângulo de elevação α.
3e00d85f-d8
UEA 2019 - Física - Cinemática, Lançamento Oblíquo

Da beirada de um penhasco, uma pessoa joga uma pedra horizontalmente com velocidade inicial v0 . A figura representa a trajetória da pedra, até atingir o solo.


Desprezando a resistência do ar e adotando g = 10 m/s² , o módulo de v0 é

A
6 m/s
B
5 m/s.
C
4 m/s.
D
2 m/s.
E
3 m/s.
119810d5-d6
EBMSP 2018 - Física - Cinemática, Lançamento Oblíquo



Um drone voa horizontalmente a 45,0m de altura do solo com velocidade de 5,0m/s quando abandona do ponto O um objeto que atinge o solo no ponto P, conforme a figura.

Considerando-se o módulo da aceleração da gravidade local igual a 10m/s2 e desprezando-se a resistência do ar, é correto afirmar:

A
O objeto atinge o ponto P dois segundos depois de ser abandonado.
B
A função horária do movimento vertical do objeto é y=45+5t–5t2.
C
O módulo da velocidade resultante do objeto no ponto P é igual a 25,0m/s.
D
O ponto P encontra-se a 20,0m de distância da vertical que passa pelo ponto O.
E
A equação da trajetória do objeto abandonado, em relação a um referencial fixo no solo, é y=1/5x2.
c646b983-b8
UECE 2014 - Física - Cinemática, Lançamento Oblíquo

Uma história em quadrinhos fala de um personagem que salta de uma altura de 30 m acima do solo, preso por um fio esticado e inextensível de 20 m de comprimento, realizando uma trajetória circular conforme a figura a seguir.



O ponto de fixação do fio também está a 30 m do solo. Despreze as forças de atrito. Considerando que o módulo da aceleração da gravidade é 10 m/s2, qual a velocidade (em m/s) do personagem no ponto mais baixo da trajetória?

A
30.
B
200.
C
20.
D
300.
e402e99a-b5
UECE 2010 - Física - Cinemática, Lançamento Oblíquo

A figura abaixo mostra quatro trajetórias de uma bola de futebol lançada no espaço.

Desconsiderando o atrito viscoso com o ar, assinale o correto.

A
A trajetória que exigiu a maior energia foi a I.
B
A trajetória que exigiu a maior energia foi a II.
C
A trajetória que exigiu a maior energia foi a III.
D
A energia exigida é a mesma para todas as trajetórias. 
c17fdf43-bb
UNEB 2014 - Física - Cinemática, Lançamento Oblíquo


Nuvens produzem chuva quando gotas minúsculas de água super-resfriadas colidem com partículas de poeira com o tamanho adequado, formando grânulos de gelo, que se precipitam em direção ao solo e derretem ao longo do caminho. O método mais conhecido de fazer chover envolve injetar partículas, “sementes” de iodeto de prata nas nuvens, em torno das quais o gelo pode se formar. (BAUM, 2014, p.46-53).


Na figura, observa-se um canhão antiaéreo, lançando obliquamente uma cápsula que contém iodeto de prata, que atinge a altura máxima na nuvem e explode. Considere o módulo da aceleração da gravidade local igual a g, a cápsula, com massa m, lançada com velocidade de módulo v0, formando um ângulo θ com a superfície horizontal. Desprezando-se a resistência do ar e com base nos conhecimentos de Física, é correto afirmar:

A
A altura atingida pela cápsula é igual a v20sen2θ/2g.
B
O movimento descrito pela cápsula é progressivo e acelerado.
C
O módulo da velocidade v0 é numericamente igual à tangente do ângulo θ.
D
A energia mecânica da cápsula no ponto mais alto da trajetória é igual a mv0cosθ/2.
E
A quantidade de movimento da cápsula imediatamente antes da explosão é igual a mv0.
6188cfbe-b9
UECE 2019 - Física - Cinemática, Lançamento Oblíquo

Em um campeonato de futebol, como o Brasileiro, de 2019, bolas são chutadas e arremessadas milhares de vezes, quase todas como lançamentos oblíquos ou variações mais elaboradas. De modo simplificado, lances de longo alcance podem ser tratados como massas puntiformes lançadas sob a ação da gravidade e da força de atrito do ar. Essa força de atrito pode, dentro de certos limites, ser tratada como proporcional ao módulo da velocidade da bola. Dado isso, é correto afirmar que

A
mesmo com a força de atrito, a trajetória continua parabólica.
B
a força de atrito tem sempre direção horizontal.
C
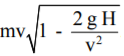o alcance de um dado lançamento é reduzido pela força de atrito.
D
a força de atrito tem sempre direção vertical.
07c85a9f-b6
UECE 2009 - Física - Cinemática, Lançamento Oblíquo

Um projétil foi lançado a partir do solo com velocidade v0 (em módulo) segundo um ângulo θ0 ≠ 0, acima da horizontal. Desprezando o atrito com o ar, o módulo da velocidade do projétil no topo da sua trajetória é:

A
v = v0 cos θ0
B
v = 0
C
v = v0 sen θ0
D
v = v0
bd69b13a-b1
FATEC 2017 - Física - Cinemática, Lançamento Oblíquo

Em um jogo de futebol, o goleiro, para aproveitar um contra-ataque, arremessa a bola no sentido do campo adversário. Ela percorre, então, uma trajetória parabólica, conforme representado na figura, em 4 segundos.


Desprezando a resistência do ar e com base nas informações apresentadas, podemos concluir que os módulos da velocidade , de lançamento, e da velocidade , na altura máxima, são, em metros por segundos, iguais a, respectivamente,

Dados:
sen β = 0,8;
cos β = 0,6.

A
15 e 25.
B
15 e 50.
C
25 e 15.
D
25 e 25.
E
25 e 50.
5170228a-b1
UEMG 2010 - Física - Lançamento Oblíquo

Uma pequena bola é arremessada segundo uma trajetória parabólica, como mostra a figura, abaixo:



Nessa figura, sendo P o ponto mais alto atingido pela bolinha, pode-se afirmar CORRETAMENTE que o vetor mostrado neste ponto P melhor representa

A
a aceleração da bolinha.
B
a força com que a bolinha foi arremessada.
C
a velocidade da bolinha.
D
a resultante das forças que atuam sobre a bolinha.
4519d5a2-dd
UFGD 2017 - Física - Cinemática, Lançamento Oblíquo

Um projétil foi disparado com um ângulo θ acima da horizontal e com uma velocidade inicial v0, em um local onde a aceleração da gravidade é igual a g. Ao chegar a sua altura máxima, depois de um tempo t, é possível afirmar, desprezando a resistência do ar, que

A
a velocidade do projétil é igual a velocidade inicial v0.
B

a distância máxima que esse projétil irá alcançar será .

C
a distância horizontal percorrida será igual a v0t.
D

a altura máxima será igual a

E
não é possível fazer afirmações, pois não se sabe a massa do projétil.