Texto 1
A MAIOR USINA SOLAR DO MUNDO FICA NO DESERTO DA CALIFÓRNIA E É CAPAZ DE
GERAR ENERGIA SUFICIENTE PARA 140 MIL CASAS
No meio do deserto da Califórnia, nos EUA, 300 mil espelhos trabalham sincronizados a um software especial para
produzir energia. Trata‐se do Ivanpah Solar Electric Generating System, a maior usina termo solar do mundo, capaz de
gerar energia suficiente para alimentar 140 mil casas.
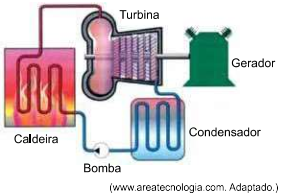
Assim como qualquer usina de energia, a Ivanpah produz energia elétrica ao criar um vapor de alta temperatura e girar
uma turbina. A diferença é que, em vez de usar energia fóssil ou nuclear para isso, é utilizado o calor do sol, que,
direcionado às torres por meio do sistema inteligente de espelhos, aquece a água, criando o vapor.
Ao todo são três unidades de geração de energia, que ocupam uma área equivalente a 14,2 quilômetros quadrados. A
Ivanpah é gerenciada pela BrightSource Limitless e pela gigante Google, que tem investido pesado em projetos
sustentáveis.
Contudo, a Ivanpah não é incrível apenas pelo seu resultado e tecnologia. Os 300 mil espelhos localizados no deserto
são também um prato cheio ao olhar, conforme revelam as imagens abaixo.
Disponível em: http://www.hypeness.com.br/2014/09/a‐maior‐usina‐solar‐do‐mundo‐e‐espetaculo‐tambem‐para‐os‐olhos/. Acesso em 27.09.15
Texto 2
Prato:
Locuções
p. cheio
fato que dá motivo para zombaria ou crítica
‹ não faça escândalo, que isso é um p. cheio para a vizinhança maledicente ›
p. comercial
m.q. prato feito ('refeição')
p. feito
1 refeição barata, a preço fixo, que já vem servida no prato e consiste ger. de um tipo de carne acompanhado de
arroz, feijão, legumes etc., e pode incluir ou não sobremesa e uma bebida não alcoólica; prato comercial, pê‐efe,
sortido
2 fig. situação favorável, fato ou conjunto de fatos que leva a determinado objetivo ou que vem a calhar para
determinado fim
‹ a vaga na empresa foi um p. feito para o jovem recém‐formado ›
p. fundo
o que tem maior profundidade e é us. para sopa; prato covo
p. raso
prato pouco profundo, us. para comida sólida
p. único
um só tipo de comida, que constitui uma refeição
Disponível em: http://houaiss.uol.com.br/busca?palavra=prato. Acesso em: 19.09.15