Questõesde PUC - SP 2017
Considere o retângulo ABCD, com AB = a, e o
triângulo EFG, com EG = a/2, FC = a/6, FG = 2√17 e DG = a/3 conforme mostra a figura.
Sabendo que os pontos A, E, F estão alinhados e
que os pontos F e G pertencem, respectivamente,
aos lados  , a área do triângulo EFG, em
unidades de área, é
, a área do triângulo EFG, em
unidades de área, é

 , a área do triângulo EFG, em
unidades de área, é
, a área do triângulo EFG, em
unidades de área, é
No encerramento de um torneio esportivo, o nome de
cada uma das 25 equipes participantes foi escrito em
um pedaço de papel e depositado em uma urna para um
sorteio. Sabendo que participaram desse torneio
7 equipes do colégio A, 9 equipes do colégio B
e 9 equipes do colégio C, então, retirando-se
aleatoriamente 2 papéis dessa urna, um após o
outro, sem reposição, a probabilidade de serem de
colégios diferentes é
A altura de um cone reto mede o dobro do raio de
sua base. Se a área lateral desse cone é 9√5 π cm2 , o volume do cone é
As notas das provas de matemática de André, Bia
e Carol formam, nessa ordem, uma progressão
geométrica de razão 1,5. Sabendo que a média
aritmética dessas três notas foi 4,75, então, a
maior nota foi
Considere as funções f(x) = 2x+k e g(x) = x2 + m, com k e m números inteiros.
Se f(1) = − 2 + g(2) e f(0) = g(0), o valor de f(g(f(-1))) é
Considere as funções f(x) = 2x+k e g(x) = x2 + m, com k e m números inteiros.
Se f(1) = − 2 + g(2) e f(0) = g(0), o valor de f(g(f(-1))) é
Uma pessoa coloca, em seu celular, uma senha de 4 dígitos, todos diferentes de zero, de modo que o
primeiro e o quarto dígitos sejam iguais, e o segundo dígito seja o dobro do terceiro. Sabendo que o
segundo e o terceiro dígitos são sempre diferentes do primeiro, então o número de possibilidades que
essa pessoa tem de montar essa senha é
As coordenadas do vértice (V) da parábola descrita pela
função f(x) = x2 − 4x + 3 também pertencem à reta r,
que é perpendicular à reta s, conforme mostra a figura.

Sabendo que o ponto A pertence à intersecção da
reta s com o eixo das ordenadas, então, a soma das
coordenadas do ponto B, que pertence à intersecção
da reta s com o eixo das abscissas, é
As coordenadas do vértice (V) da parábola descrita pela função f(x) = x2 − 4x + 3 também pertencem à reta r, que é perpendicular à reta s, conforme mostra a figura.

Sabendo que o ponto A pertence à intersecção da
reta s com o eixo das ordenadas, então, a soma das
coordenadas do ponto B, que pertence à intersecção
da reta s com o eixo das abscissas, é
O matemático Al-Karkhî escreveu um trabalho sobre
álgebra, no qual descreve uma técnica de encontrar
números racionais x, y, z, não nulos, tais que x3
+ y3
= z2.
Nesse trabalho ele utiliza ,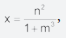 , y = m x e z = n x, com m e n números racionais quaisquer, não nulos.
, y = m x e z = n x, com m e n números racionais quaisquer, não nulos.
Fonte: Introdução à História da Matemática. Howard Eves. Ed. UNICAMP. Adaptado
Adotando m = 2 e sabendo que x + y = z, o valor
de (x + y)z é um número
O matemático Al-Karkhî escreveu um trabalho sobre
álgebra, no qual descreve uma técnica de encontrar
números racionais x, y, z, não nulos, tais que x3
+ y3
= z2.
Nesse trabalho ele utiliza ,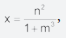 , y = m x e z = n x, com m e n números racionais quaisquer, não nulos.
, y = m x e z = n x, com m e n números racionais quaisquer, não nulos.
Fonte: Introdução à História da Matemática. Howard Eves. Ed. UNICAMP. Adaptado
Adotando m = 2 e sabendo que x + y = z, o valor
de (x + y)z é um número