Questõesde UNIOESTE 2017 sobre Matemática
Em uma área de proteção ambiental existe uma população de coelhos. Com o aumento natural da
quantidade de coelhos, há muita oferta de alimento para os predadores. Os predadores com a oferta de
alimento também aumentam seu número e abatem mais coelhos. O número de coelhos volta então a cair.
Forma-se assim um ciclo de oscilação do número de coelhos nesta reserva. Considerando-se que a população p(t) de coelhos fica bem modelada por p(t) = 1000 - 250sen  , sendo > ≥ 0 a quantidade de dias
decorridos, e o argumento da função seno é medido em radianos, pode-se afirmar que
, sendo > ≥ 0 a quantidade de dias
decorridos, e o argumento da função seno é medido em radianos, pode-se afirmar que
Em uma área de proteção ambiental existe uma população de coelhos. Com o aumento natural da
quantidade de coelhos, há muita oferta de alimento para os predadores. Os predadores com a oferta de
alimento também aumentam seu número e abatem mais coelhos. O número de coelhos volta então a cair.
Forma-se assim um ciclo de oscilação do número de coelhos nesta reserva. Considerando-se que a população p(t) de coelhos fica bem modelada por p(t) = 1000 - 250sen  , sendo > ≥ 0 a quantidade de dias
decorridos, e o argumento da função seno é medido em radianos, pode-se afirmar que
, sendo > ≥ 0 a quantidade de dias
decorridos, e o argumento da função seno é medido em radianos, pode-se afirmar que
A Figura 1 apresenta uma sequência de figuras de bonecos com corpo e pernas no formato retangular e
cabeça circular. As dimensões do primeiro boneco são apresentadas na Figura 2 (Na Figura 2, r é o raio do
círculo). Sabe-se que cada uma das medidas do n-ésimo boneco é igual à metade da medida correspondente
do (n-1)-ésimo boneco. Assim, se A1 é a área do primeiro boneco, então é CORRETO afirmar que a soma
das áreas dos 30 primeiros bonecos é







As raízes do polinômio P(x) = x4 + bx3 + cx2 + dx + e, são iguais a i, -i, 3 e 1/2. Sobre P(x), pode-se então afirmar que
Existem dois valores reais, a1 e a2, que a pode assumir de modo que a equação matricial 
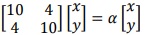 admita solução não trivial. Assim, é CORRETO afirmar que
admita solução não trivial. Assim, é CORRETO afirmar que
Existem dois valores reais, a1 e a2, que a pode assumir de modo que a equação matricial 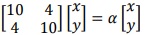 admita solução não trivial. Assim, é CORRETO afirmar que
admita solução não trivial. Assim, é CORRETO afirmar que
a1 ∈ Z, a2 ∈ Z e a1 . a2 = 20.