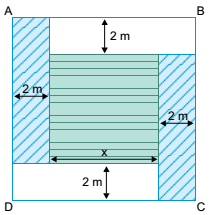
Um cubo com aresta de medida igual a x centímetros foi seccionado, dando origem ao prisma indicado na figura 1. A figura 2 indica a vista superior desse prisma, sendo que AEB é um triângulo equilátero.

Sabendo-se que o volume do prisma da figura 1 é igual a 2(4 - √3)cm3 , x é igual a
Um cubo com aresta de medida igual a x centímetros foi seccionado, dando origem ao prisma indicado na figura 1. A figura 2 indica a vista superior desse prisma, sendo que AEB é um triângulo equilátero.

Sabendo-se que o volume do prisma da figura 1 é igual a 2(4 - √3)cm3 , x é igual a
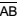 e
e 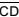 , conforme indica a figura. Sabe-se que AB = CD = 1 m, e que M é ponto médio dos segmentos coplanares
, conforme indica a figura. Sabe-se que AB = CD = 1 m, e que M é ponto médio dos segmentos coplanares 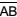 e
e 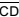 . Quando a mesa está armada, o tampo fica paralelo ao plano do chão e a medida do ângulo
. Quando a mesa está armada, o tampo fica paralelo ao plano do chão e a medida do ângulo 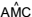 é 60º.
é 60º.