Questõesde UNESP 2010 sobre Matemática
ma pessoa se encontra no ponto A de uma planície, às margens de um rio e vê, do outro lado do rio, o topo do mastro de uma bandeira, ponto B. Com o objetivo de determinar a altura h do mastro, ela anda, em linha reta, 50 m para a direita do ponto em que se encontrava e marca o ponto C. Sendo D o pé do mastro, avalia que os ângulos BÂC e BĈD valem 30º, e o ângulo AĈB vale 105º, como mostra a figura.
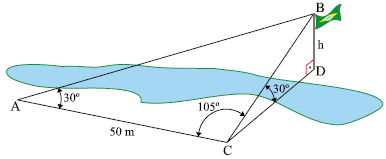
A altura h do mastro da bandeira, em metros, é:

Após o nascimento do filho, o pai comprometeu-se a depositar mensalmente, em uma caderneta de poupança, os valores de R$ 1,00, R$ 2,00, R$ 4,00 e assim sucessivamente, até o mês em que o valor do depósito atingisse R$ 2.048,00. No mês seguinte o pai recomeçaria os depósitos como de início e assim o faria até o 21º aniversário do filho. Não tendo ocorrido falha de depósito ao longo do período, e sabendo-se que 210 = 1.024, o montante total dos depósitos, em reais, feitos em caderneta de poupança foi de:
Ambientalistas, após estudos sobre o impacto que possa vir a ser causado à população de certa espécie de pássaros pela construção de um grande conjunto de edifícios residenciais próximo ao sopé da Serra do Japi, em Jundiaí, SP, concluíram que a quantidade de tais pássaros, naquela região, em função do tempo, pode ser expressa, aproximadamente, pela função

onde t representa o tempo, em anos, e P0 a população de pássaros na data de início da construção do conjunto. Baseado nessas informações, pode-se afirmar que:

A família acabou comprando a TV, o freezer e a churrasqueira nestas três lojas. O valor total pago, em reais, pelos três produtos foi de:
Baseado no gráfico, pode-se concluir que os 20% mais pobres da população brasileira detêm 3,5% (1%+2,5%) da renda nacional. Supondo a população brasileira igual a 200 milhões de habitantes e o PIB brasileiro igual a 2,4 trilhões de reais (Fonte: IBGE), a renda per capita dos 20% mais ricos da população brasileira, em reais, é de:

Os professores de matemática e educação física de uma escola organizaram um campeonato de damas entre os alunos. Pelas regras do campeonato, cada colocação admitia apenas um ocupante. Para premiar os três primeiros colocados, a direção da escola comprou 310 chocolates, que foram divididos entre os 1.º, 2.º e 3.º colocados no campeonato, em quantidades inversamente proporcionais aos números 2, 3 e 5, respectivamente. As quantidades de chocolates recebidas pelos alunos premiados, em ordem crescente de colocação no campeonato, foram:
Em um experimento sobre orientação e navegação de pombos,considerou-se o pombal como a origem O de um sistema de coordenadas cartesianas e os eixos orientados Sul-Norte (SN) e Oeste-Leste (WL). Algumas aves foram liberadas num ponto P que fica 52 km ao leste do eixo SN e a 30 km ao sul do eixo WL. O ângulo azimutal de P é o ângulo, em graus, medido no sentido horário a partir da semirreta ON até a semirreta OP. No experimento descrito, a distância do pombal até o ponto de liberação das aves, em km, e o ângulo azimutal, em graus, desse ponto são,respectivamente:
Dado: √3604 ≈ 60.

Em um experimento sobre orientação e navegação de pombos,considerou-se o pombal como a origem O de um sistema de coordenadas cartesianas e os eixos orientados Sul-Norte (SN) e Oeste-Leste (WL). Algumas aves foram liberadas num ponto P que fica 52 km ao leste do eixo SN e a 30 km ao sul do eixo WL. O ângulo azimutal de P é o ângulo, em graus, medido no sentido horário a partir da semirreta ON até a semirreta OP. No experimento descrito, a distância do pombal até o ponto de liberação das aves, em km, e o ângulo azimutal, em graus, desse ponto são,respectivamente:
Dado: √3604 ≈ 60.

Através dos gráficos das funções f(x) e g(x), os valores de f(g(0))
e g(f(1)) são, respectivamente:

Através dos gráficos das funções f(x) e g(x), os valores de f(g(0)) e g(f(1)) são, respectivamente:

Em situação normal, observa-se que os sucessivos períodos de
aspiração e expiração de ar dos pulmões em um indivíduo são
iguais em tempo, bem como na quantidade de ar inalada e expelida.
A velocidade de aspiração e expiração de ar dos pulmões de um
indivíduo está representada pela curva do gráfico, considerando
apenas um ciclo do processo.

Sabendo-se que, em uma pessoa em estado de repouso, um ciclo
de aspiração e expiração completo ocorre a cada 5 segundos e
que a taxa máxima de inalação e exalação, em módulo, é 0,6 l/s,
a expressão da função cujo gráfico mais se aproxima da curva
representada na figura é:
Em situação normal, observa-se que os sucessivos períodos de aspiração e expiração de ar dos pulmões em um indivíduo são iguais em tempo, bem como na quantidade de ar inalada e expelida.
A velocidade de aspiração e expiração de ar dos pulmões de um indivíduo está representada pela curva do gráfico, considerando apenas um ciclo do processo.

Sabendo-se que, em uma pessoa em estado de repouso, um ciclo
de aspiração e expiração completo ocorre a cada 5 segundos e
que a taxa máxima de inalação e exalação, em módulo, é 0,6 l/s,
a expressão da função cujo gráfico mais se aproxima da curva
representada na figura é:





O papelão utilizado na fabricação de caixas reforçadas é composto
de três folhas de papel, coladas uma nas outras, sendo que
as duas folhas das faces são “lisas” e a folha que se intercala
entre elas é “sanfonada”, conforme mostrado na figura.

O fabricante desse papelão compra o papel em bobinas, de comprimento
variável. Supondo que a folha “sanfonada” descreva
uma curva composta por uma sequência de semicircunferências,
com concavidades alternadas e de raio externo (RExt) de 1,5 mm,
determine qual deve ser a quantidade de papel da bobina que gerará
a folha “sanfonada”, com precisão de centímetros, para que,
no processo de fabricação do papelão, esta se esgote no mesmo
instante das outras duas bobinas de 102 m de comprimento de
papel, que produzirão as faces “lisas”.
Dado: π ≈ 3,14.
O papelão utilizado na fabricação de caixas reforçadas é composto de três folhas de papel, coladas uma nas outras, sendo que as duas folhas das faces são “lisas” e a folha que se intercala entre elas é “sanfonada”, conforme mostrado na figura.

O fabricante desse papelão compra o papel em bobinas, de comprimento variável. Supondo que a folha “sanfonada” descreva uma curva composta por uma sequência de semicircunferências, com concavidades alternadas e de raio externo (RExt) de 1,5 mm, determine qual deve ser a quantidade de papel da bobina que gerará a folha “sanfonada”, com precisão de centímetros, para que, no processo de fabricação do papelão, esta se esgote no mesmo instante das outras duas bobinas de 102 m de comprimento de papel, que produzirão as faces “lisas”.
Dado: π ≈ 3,14.
Observe o gráfico da função f(x) e analise as afirmações a seu
respeito.

I. Se x1
, x2 ∈ Dom(f) e x2
> x1
, então f(x2
) > f(x1
).
II. Se x > 1, então f(x) < 0.
III. O ponto (2, –2) pertence ao gráfico de f(x).
IV. A lei de formação de f(x) representada no gráfico é dada
por f(x) = - 1/2 ( x -1).
A alternativa que corresponde a todas as afirmações verdadeiras é:
Observe o gráfico da função f(x) e analise as afirmações a seu respeito.

I. Se x1 , x2 ∈ Dom(f) e x2 > x1 , então f(x2 ) > f(x1 ).
II. Se x > 1, então f(x) < 0.
III. O ponto (2, –2) pertence ao gráfico de f(x).
IV. A lei de formação de f(x) representada no gráfico é dada por f(x) = - 1/2 ( x -1).
A alternativa que corresponde a todas as afirmações verdadeiras é:
Uma aeronave faz sua aproximação final do destino, quando seu
comandante é informado pelo controlador de voo que, devido ao
intenso tráfego aéreo, haverá um tempo de espera de 15 minutos
para que o pouso seja autorizado e que ele deve permanecer em
rota circular, em torno da torre de controle do aeroporto, a 1500
metros de altitude, até que a autorização para o pouso seja dada.
O comandante, cônscio do tempo de espera a ser despendido e
de que, nessas condições, a aeronave que pilota voa a uma velocidade
constante de Vc
(km/h), decide realizar uma única volta
em torno da torre de controle durante o tempo de espera para
aterrissar.
Sabendo que o aeroporto encontra-se numa planície e tomando
sua torre de controle como sendo o ponto de origem de um sistema
de coordenadas cartesianas, determine a equação da projeção
ortogonal, sobre o solo, da circunferência que a aeronave descreverá
na altitude especificada.

Uma aeronave faz sua aproximação final do destino, quando seu comandante é informado pelo controlador de voo que, devido ao intenso tráfego aéreo, haverá um tempo de espera de 15 minutos para que o pouso seja autorizado e que ele deve permanecer em rota circular, em torno da torre de controle do aeroporto, a 1500 metros de altitude, até que a autorização para o pouso seja dada. O comandante, cônscio do tempo de espera a ser despendido e de que, nessas condições, a aeronave que pilota voa a uma velocidade constante de Vc (km/h), decide realizar uma única volta em torno da torre de controle durante o tempo de espera para aterrissar.
Sabendo que o aeroporto encontra-se numa planície e tomando sua torre de controle como sendo o ponto de origem de um sistema de coordenadas cartesianas, determine a equação da projeção ortogonal, sobre o solo, da circunferência que a aeronave descreverá na altitude especificada.






No Brasil, desde junho de 2008, se for constatada uma concentração
de álcool no sangue acima de 0,6 g/l, o motorista é detido
e processado criminalmente.
(www.planalto.gov.br/ccivil_03/Ato2007-2010/2008/
Decreto/D6488.htm. Adaptado.)
Determine o número máximo de latas de cerveja que um motorista
pode ingerir, antes de dirigir, para não ser processado criminalmente
caso seja submetido ao teste.
Dados:
– o volume médio de sangue no corpo de um homem
adulto é 7,0 litros;
– uma lata de cerveja de 350 ml contém 16 ml de álcool;
– 14% do volume de álcool ingerido por um homem
adulto vão para a corrente sanguínea;
– a densidade do álcool contido em cervejas é de 0,8 g/ml.
Observação: Os resultados de todas as operações devem ser
aproximados por duas casas decimais.
No Brasil, desde junho de 2008, se for constatada uma concentração de álcool no sangue acima de 0,6 g/l, o motorista é detido e processado criminalmente.
(www.planalto.gov.br/ccivil_03/Ato2007-2010/2008/
Decreto/D6488.htm. Adaptado.)
Determine o número máximo de latas de cerveja que um motorista pode ingerir, antes de dirigir, para não ser processado criminalmente caso seja submetido ao teste.
Dados:
– o volume médio de sangue no corpo de um homem adulto é 7,0 litros;
– uma lata de cerveja de 350 ml contém 16 ml de álcool;
– 14% do volume de álcool ingerido por um homem adulto vão para a corrente sanguínea;
– a densidade do álcool contido em cervejas é de 0,8 g/ml.
Observação: Os resultados de todas as operações devem ser aproximados por duas casas decimais.
Paulo quer comprar um sorvete com 4 bolas em uma sorveteria
que possui três sabores de sorvete: chocolate, morango e uva. De
quantos modos diferentes ele pode fazer a compra?
Você está fazendo um ‘tour’ turístico pelo centro da cidade de São
Paulo, visitando pontos históricos e museus. O ponto de saída é a
Praça da Luz, na Estação da Luz. Seu roteiro segue pela Pinacoteca
do Estado, Museu de Arte Sacra e termina no Pátio do Colégio.

Para percorrer todo o trajeto, a distância, em metros, que terá de
fazer é, aproximadamente,
Você está fazendo um ‘tour’ turístico pelo centro da cidade de São Paulo, visitando pontos históricos e museus. O ponto de saída é a Praça da Luz, na Estação da Luz. Seu roteiro segue pela Pinacoteca do Estado, Museu de Arte Sacra e termina no Pátio do Colégio.

Para percorrer todo o trajeto, a distância, em metros, que terá de
fazer é, aproximadamente,