c83c3654-49
UNB 2010 - Matemática - Função Logarítmica, Funções
A função f não está definida em N = 1.
A função f não está definida em N = 1.
Considerando a função dada por  julgue o item que se segue.
julgue o item que se segue.
 julgue o item que se segue.
julgue o item que se segue.C
Certo
E
Errado
 julgue o item que se segue.
julgue o item que se segue.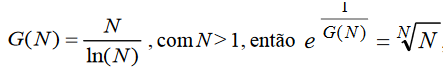 , em que e é a base do logaritmo natural.
, em que e é a base do logaritmo natural.





Determine qual é o vigésimo primeiro número primo,
quando os números são listados em ordem crescente
de valor


Para a densidade DN definida no texto, é válida a relação .
DN = DN2 + DN3.








Escolhendo-se ao acaso um número natural de 1 a 1.000, a probabilidade de ele ser primo é menor que da
1⁄ 4 probabilidade de haver pelo menos duas pessoas que façam aniversário no mesmo mês em uma sala que tenha 6 indivíduos, assumindo-se que não há gêmeos, que o mês tem 30 dias e que as datas de aniversários são equiprováveis.








