Leia as afirmações que seguem e marque “V” para verdadeiro ou “F” para falso, nos parênteses, e, depois,
assinale a alternativa correta.
( ) Todo paralelogramo é um quadrilátero.
( ) Todo trapézio é um quadrilátero.
( ) Todo losango é um quadrado.
( ) Existe retângulo que não é quadrado.
Leia as afirmações que seguem e marque “V” para verdadeiro ou “F” para falso, nos parênteses, e, depois, assinale a alternativa correta.
( ) Todo paralelogramo é um quadrilátero.
( ) Todo trapézio é um quadrilátero.
( ) Todo losango é um quadrado.
( ) Existe retângulo que não é quadrado.
 , o número de ouro, que também está presente nas sinfonias 5 e 9 de Ludwig van Beethoven. Os cartões
de crédito utilizam, na sua confecção, esta proporção.
, o número de ouro, que também está presente nas sinfonias 5 e 9 de Ludwig van Beethoven. Os cartões
de crédito utilizam, na sua confecção, esta proporção.




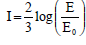 onde E é a energia liberada no terremoto em quilowatt-hora e E
onde E é a energia liberada no terremoto em quilowatt-hora e E