Questõesde UFVJM-MG sobre Matemática

InícioTodas as questões
1
1
Foram encontradas 103 questões
f4ab4f69-d9
UFVJM-MG 2017 - Matemática - Áreas e Perímetros, Geometria Plana

A pousada Castelinho, da cidade Diamantina (MG), promoveu uma festa no espaço de recreação em suas dependências. Se considerarmos que, para a segurança do evento, a densidade média seja de 3 pessoas por metro quadrado e sabendo que esse espaço tem o formato de um quadrado menor e um quadrado maior, respectivamente, medindo 12 metros e 22 metros de lado, dispostos como indicado na figura abaixo, o número máximo de pessoas que o evento deve receber para garantir a segurança é de:


A
264
B
916
C
1056
D
1884
f4ae5633-d9
UFVJM-MG 2017 - Matemática - Aritmética e Problemas, Razão, Proporção e Números Proporcionais

Em Diamantina, há 20 mil torcedores do Atlético Mineiro. Dentre esses, 5 mil também torcem para o Barcelona. Sabendo que a população de Diamantina é de 42 mil habitantes e que 14 mil não torcem nem para o Atlético Mineiro e nem para o Barcelona, então, o número de habitantes que torcem para o Barcelona é:

A
8 mil
B
12 mil
C
13 mil
D
20 mil
f4b2cb31-d9
UFVJM-MG 2017 - Matemática - Aritmética e Problemas, Regra de Três

Em uma floricultura, duas garotas trabalham como floristas. A mais experiente consegue embalar 120 tulipas em 40 minutos. A outra consegue embalar a mesma quantidade de tulipas em 60 minutos. Se as duas se dedicarem juntas a embalar 120 tulipas, o tempo que elas gastarão será de:

A
20 min
B
24 min
C
36 min
D
50 min
f4b5ef65-d9
UFVJM-MG 2017 - Matemática - Quadriláteros, Geometria Plana

Um carpinteiro fez um desenho de uma bancada para maximizar o espaço livre de uma cozinha, formada pela junção de dois trapézios. Considerando que a bancada tem 1 metro de largura; a base menor do trapézio (T1) é o dobro da base menor do trapézio 2 (T2) e que a base maior do trapézio 1 (T1) mede 3m, á área total da bancada é:


A
2 m²
B
3 m²
C
4 m²
D
5 m²
f4a221ef-d9
UFVJM-MG 2017 - Matemática - Geometria Plana, Triângulos

Um estabelecimento comercial precisou fazer algumas adaptações às normas de acessibilidade de forma a tornar o ambiente acessível a alguns clientes que são portadores de necessidades especiais. Para projetar a rampa de acesso foi contratado um especialista que apresentou a seguinte fórmula para os cálculos



Onde i é a inclinação (em porcentagem), h a altura do desnível e c o comprimento da projeção horizontal conforme a figura a seguir. Após algumas medidas constatou-se que a rampa ideal para o estabelecimento será construída de forma que θ= 30º.



Usando √3 = 1,7 , podemos afirmar que a inclinação (i) será de aproximadamente:

A
17%.
B
27%.
C
57%.
D
100%.
f49bf74b-d9
UFVJM-MG 2017 - Matemática - Funções, Função de 2º Grau

figura a seguir representa graficamente, no plano cartesiano, uma função de 2º grau f(x) = ax² + bx + c , em que a , b e c são constantes reais.



De acordo com a figura, a afirmação CORRETA é:

A
a c > 0.
B
b c < 0.
C
a b c < 0.
D
4 a c > b².
f498c067-d9
UFVJM-MG 2017 - Matemática - Funções, Função de 1º Grau

O responsável pela venda de uma peça em uma empresa observou que o lucro, em reais, na venda dessa peça, pode ser modelado pela função f (x) = a x + b . Sabe-se que a e b são constantes reais e x é um número inteiro do intervalo [ 0 , 80 ] que representa o número de peças. Se ao produzir 6 peças o lucro foi de R$950,00 e ao produzir 23 peças o lucro foi de R$3.500,00, então, o lucro na venda do maior número dessas peças será de:

A
R$ 4.150,00.
B
R$ 6.450,00.
C
R$ 8.050,00.
D
R$ 12.050,00.
5ebe76f8-b6
UFVJM-MG 2016 - Matemática - Limite

Suponhamos que durante o mês de fevereiro de 2016 o crescimento exponencial seja dado pela fórmula P(t) = P(0) er.t , onde P(t) é a população infectada após t semanas e P(0) representa a quantidade de pessoas inicialmente infectadas.

Se após as duas primeiras semanas de fevereiro a quantidade de pessoas infectadas dobrou e usando ln(2) = 0,7 pode-se afirmar que o valor da constante r é

Uma pesquisa feita em São Paulo acerca do avanço da dengue pela Secretaria Municipal de Saúde (SMS), constatou que de 01/01/2016 até o dia 12/03/2016 o número de pessoas infectadas supera em 92% o total registrado no mesmo período do ano passado. O monitoramento semanal feito pela SMS mostra um crescimento exponencial do problema.

http://vejasp.abril.com.br/materia/dengue-rotina-paulistanos

A
0,35
B
0,49
C
0,70
D
1,40
5ecae142-b6
UFVJM-MG 2016 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas, Áreas e Perímetros, Regra de Três, Geometria Plana

De acordo com esses dados, pode-se afirmar que o tempo necessário, em segundos, para que a Hidrelétrica consiga armazenar 1695m3 é:

Os dados da Hidrelétrica de Três Marias, divulgados pela Cemig no dia 29 de março, mostram que a vazão de água afluente (quantidade de água que entra por segundo) foi de 440 m3 /s e a vazão de água defluente (quantidade de água que sai por segundo) foi de 101m3 /s.

Fonte:https://www.cemig.com.br/pt-br/a_cemig/nossos_negocios/usinas/ Paginas/Três_Marias_dados.aspx

A
3 segundos.
B
4 segundos.
C
5 segundos.
D
6 segundos.
5ec25f77-b6
UFVJM-MG 2016 - Matemática - Áreas e Perímetros, Geometria Plana

Uma piscina olímpica é o tipo de piscina adequada para a prática de desportos olímpicos. A Federação Internacional de Natação estabelece que as piscinas olímpicas tenham 50 metros de comprimento.

Uma marcação encontra-se projetada na superfície da água de uma piscina retangular exatamente na metade de seu comprimento, ou seja, localizada a 25 metros das margens que delimitam o comprimento da piscina.

Um nadador parte da margem esquerda (A), nadando em linha reta no sentindo da margem direita (B), como indicado nesta figura.


Fonte:https://pt.wikipedia.org/wiki/Piscina_ol%C3%ADmpica.

Acesso em 03 de março de 2016, adaptado.


Em um dado instante, X denota a distância (em metros) do nadador à margem A.

Nesse instante, a distância (em metros) do nadador à marcação projetada na superfície da piscina é:

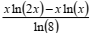A
x - 25
B
25 - x
C
|x - 25|
D
|x + 25|
5ec6a435-b6
UFVJM-MG 2016 - Matemática - Áreas e Perímetros, Geometria Plana

Uma viga AB deverá ser colocada entre dois corredores para sustentação de um telhado, como indicado na figura a seguir.



Considerando que um dos corredores possui 5 m e o outro 3 m de largura, o comprimento máximo da viga AB é:

A
10√3 + 2 m
B
2(5 + 9√3) /3 m
C
10 + 2√3 m
D
2(5√3 + 9) / 3 m
5eb98242-b6
UFVJM-MG 2016 - Matemática - Áreas e Perímetros, Geometria Plana

O proprietário de um estabelecimento comercial encomendou ao seu decorador um painel retangular de dimensões 240 cm e 270 cm. Porém, exigiu que seu painel fosse formado com placas idênticas, quadradas e com dimensões inteiras, em centímetros.

Dessa forma, o menor número de placas quadradas necessário para preencher esse painel nas condições estabelecidas, de maneira que não haja cortes ou sobras de material, é:

A
72
B
108
C
162
D
216
5eb03eaf-b6
UFVJM-MG 2016 - Matemática - Análise de Tabelas e Gráficos, Funções, Função de 2º Grau

Este gráfico mostra uma análise da cotação do dólar do dia 23 ao dia 28 de março de 2016.


Fonte:http://economia.uol.com.br/cotacoes/cambio/dolar-comercial-estados-unidos


A função que representa esse gráfico é do tipo


Com base nesse gráfico e nas informações apresentadas, pode-se afirmar que

A
ƒ(x) é crescente
B
d < b
C
a > 0 e c < 0
D
a < 0 e b > 0
5eb495d4-b6
UFVJM-MG 2016 - Matemática - Circunferências e Círculos, Geometria Plana

Em um parque de diversão, Pedro e Marta resolveram brincar em uma roda gigante que contém 8 bancos (individuais) igualmente espaçados e que gira no sentido anti-horário, conforme demonstrado nesta figura.



Para ocupar todos os bancos, cada criança foi colocada no brinquedo, pela rampa de acesso, de maneira organizada (uma a uma) sem saltar nenhum banco. Pedro sentou-se no banco A e Marta, que foi a última a entrar, sentou-se no banco D. Todos os lugares foram ocupados.

Quando Marta completou 4 voltas completas (1440°), a distância percorrida por Pedro, em graus, era de:

A
1485
B
1530
C
1665
D
1710
5ea8f4ef-b6
UFVJM-MG 2016 - Matemática - Funções, Equação Logarítmica

Durante uma aula de Cálculo para os cursos de Engenharia, o professor se deparou com a expressão .

Muitos alunos tiveram dúvidas e o professor deu a dica: “vocês devem usar as propriedades de logaritmo para simplificar essa expressão”.

Ao simplificar essa expressão, o resultado correto, é:

A
x / In(8)
B
2x / In(2)
C
x/2
D
x/3
af2d153b-b6
UFVJM-MG 2017 - Matemática - Análise de Tabelas e Gráficos, Álgebra Linear - Equações Lineares, Espaço Vetorial e Transformações Lineares e Matrizes, Pontos e Retas, Geometria Analítica, Álgebra Linear

O hipercentro de Belo Horizonte foi planejado em uma região plana com ruas paralelas e perpendiculares, delimitando quadras do mesmo tamanho. Em março de 2014 foi inaugurado o MOVE que é um sistema de transporte rápido por ônibus, constituído por uma rede de corredores exclusivos e estações de integração e de transferência ao longo do hipercentro. Consideremos que as avenidas Amazonas e Afonso Pena representem os eixos coordenados de um plano cartesiano e a reta de equação y = x + 2 represente o trajeto do MOVE que atravessa o hipercentro. No ponto (0, 3) localiza-se a rodoviária.

O ponto em que deve ser construída uma estação do MOVE para que a distância até a rodoviária não seja maior que duas quadras é:



A
(1, 3)
B
(-2, 0)
C
(-1, 1)
D
(1, -1)
af249743-b6
UFVJM-MG 2017 - Matemática - Geometria Espacial, Cilindro

Uma embalagem tem formato de um cilindro com raio da base medindo 6 centímetros e volume de 432 π cm3 . Será produzida uma nova embalagem, com mesmo formato e volume, de tal modo que o raio da base seja 50% menor. Sendo assim, a altura da nova embalagem será

A
18 cm.
B
22 cm.
C
48 cm.
D
66 cm.
af1b4cac-b6
UFVJM-MG 2017 - Matemática - Probabilidade

Para uma prova de seleção em um concurso para professores foi disponibilizado um edital contendo dez conteúdos. A organização do concurso optou por um sorteio que irá definir, no dia da prova, os dois conteúdos sobre os quais os concorrentes serão avaliados. Paulo resolveu participar do concurso, mas só conseguiu estudar sete dos conteúdos previstos no edital.

MARQUE a alternativa que indica a probabilidade de ser sorteado, no dia da prova, pelo menos um conteúdo que Paulo estudou.

A
1/15
B
7/15
C
14/15
D
7/30
af15e0cf-b6
UFVJM-MG 2017 - Matemática - Análise de Tabelas e Gráficos, Aritmética e Problemas, Porcentagem

O Brasil vive uma epidemia de Sifilis, constatando um aumento de mais de 5000% no número de casos nos últimos 5 anos. A Sífilis é uma doença infecciosa transmitida pela bactéria treponema pallidum cuja transmissão ocorre, basicamente, durante a relação sexual ou de mãe para filho, pelo sangue, durante a gravidez. A tabela abaixo mostra a evolução do número de casos de Sífilis notificados no estado de Minas Gerais nos últimos 10 anos.



De acordo com os dados da tabela acima nota-se que o maior aumento percentual aconteceu no número de casos de Sífilis adquirida de 2007 para 2011 (superior a 4000%).

É CORRETO afirmar que o menor aumento percentual aconteceu no número de casos notificados de:

A
Sífilis Gestante de 2007 para 2011
B
Sífilis Gestante de 2011 para 2016
C
Sífilis Congênita de 2007 para 2011
D
Sífilis Congênita de 2011 para 2016
af110db5-b6
UFVJM-MG 2017 - Matemática - Matrizes, Álgebra Linear

Uma microempresária produz três tipos de bolos, B1 , B2 e B3 . Esses bolos são vendidos em duas padarias de sua cidade, P1 e P2 . A matriz a seguir fornece a quantidade de bolos B1 , B2 e B3 vendidos a cada uma das padarias P1 e P2 , no mês de janeiro.



No referido mês, os lucros obtidos pela microempresária com a venda dos bolos às padarias P1 e P2 foi de R$1.333,00 e R$ 1.041,00, respectivamente. O lucro obtido pela microempresária com a venda de cada bolo B3 é de R$21,00.


Já o lucro obtido pela microempresária com a venda de cada um dos bolos B1 e B2 é, respectivamente, de:

A
R$ 22,00 e R$ 36,00.
B
R$ 24,00 e R$ 34,00.
C
R$ 28,00 e R$ 32,00.
D
R$ 30,00 e R$ 27,00.