f804a0d5-49
UFRN 2010, UFRN 2010, UFRN 2010 - Matemática - Geometria Espacial, Poliedros
Como parte da decoração de sua sala de trabalho, José colocou sobre uma mesa um aquário de acrílico em forma de paralelepípedo retângulo, com dimensões medindo 20cm x 30cm x 40cm. Com o aquário apoiado sobre a face de dimensões 40cm x 20cm, o nível da água ficou a 25cm de altura.
Se o aquário fosse apoiado sobre a face de dimensões 20cm x 30cm, a altura da água, mantendo-se o mesmo volume, seria de, aproximadamente,
Como parte da decoração de sua sala de trabalho, José colocou sobre uma mesa um aquário de acrílico em forma de paralelepípedo retângulo, com dimensões medindo 20cm x 30cm x 40cm. Com o aquário apoiado sobre a face de dimensões 40cm x 20cm, o nível da água ficou a 25cm de altura.
Se o aquário fosse apoiado sobre a face de dimensões 20cm x 30cm, a altura da água, mantendo-se o mesmo volume, seria de, aproximadamente,
Se o aquário fosse apoiado sobre a face de dimensões 20cm x 30cm, a altura da água, mantendo-se o mesmo volume, seria de, aproximadamente,
A
16cm.
B
17cm.
C
33cm.
D
35cm.



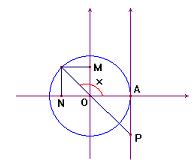
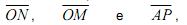 correspondem, respectivamente, a
correspondem, respectivamente, a 


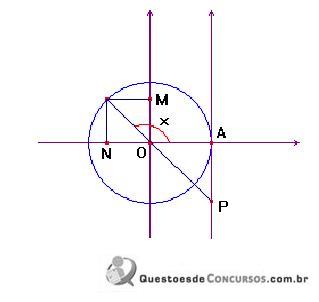
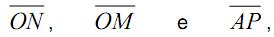 correspondem, respectivamente, a
correspondem, respectivamente, a 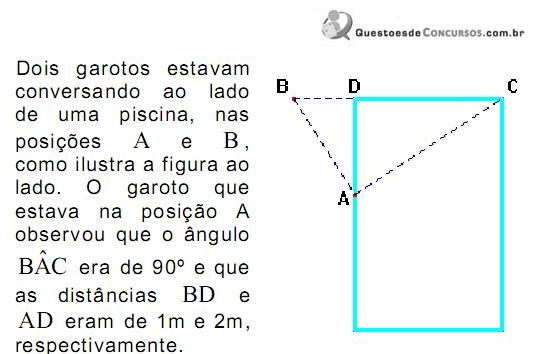

 , nas condições acima, tiver uma única solução, as respectivas retas
, nas condições acima, tiver uma única solução, as respectivas retas