02345fe3-49
UFRN 2010, UFRN 2010, UFRN 2010 - Matemática - Probabilidade
Um empresário contribui financeiramente para uma instituição filantrópica e a visita semanalmente, sendo o dia da semana escolhido aleatoriamente.
Em duas semanas consecutivas, a probabilidade de a visita ocorrer no mesmo dia da semana é
Um empresário contribui financeiramente para uma instituição filantrópica e a visita semanalmente, sendo o dia da semana escolhido aleatoriamente.
Em duas semanas consecutivas, a probabilidade de a visita ocorrer no mesmo dia da semana é
Em duas semanas consecutivas, a probabilidade de a visita ocorrer no mesmo dia da semana é
A
três vezes a probabilidade de ocorrer em dois dias distintos.
B
um terço da probabilidade de ocorrer em dois dias distintos.
C
seis vezes a probabilidade de ocorrer em dois dias distintos.
D
um sexto da probabilidade de ocorrer em dois dias distintos.

 para t ≥ 0 .
para t ≥ 0 .  é maior que o de
é maior que o de  .
. é menor que o de
é menor que o de 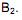 .
. aumenta 10% e o de
aumenta 10% e o de  aumenta 90%.
aumenta 90%. cresce 20 vezes menos que o de
cresce 20 vezes menos que o de  .
. são paralelas entre si.
são paralelas entre si. 
 e quer ir para a rua
e quer ir para a rua  até à posição B.
até à posição B.

