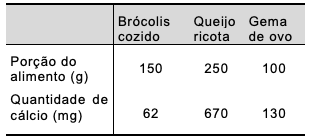
Um tanque cilíndrico, cheio de combustível,
de raio, R = 1 m e
altura, H = 4 m, ao
ser suspenso por um
cabo de aço fixado
no ponto P, inclinouse até a posição
mostrada na figura.
Parte do combustível
foi derramado, de
modo que o restante
ficou nivelado como
se vê na figura ao
lado.
A quantidade de combustível que restou no
tanque foi, aproximadamente:

Um tanque cilíndrico, cheio de combustível, de raio, R = 1 m e altura, H = 4 m, ao ser suspenso por um cabo de aço fixado no ponto P, inclinouse até a posição mostrada na figura. Parte do combustível foi derramado, de modo que o restante ficou nivelado como se vê na figura ao lado.
A quantidade de combustível que restou no
tanque foi, aproximadamente:
 , é correto afirmar:
, é correto afirmar: 


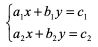 com a
com a