O valor de
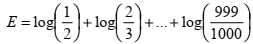 é .
é .
O valor de
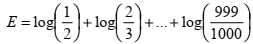 é .
é .
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
O valor de
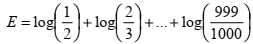 é .
é .
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
O gráfico de ƒ(x) está esboçado na imagem a seguir.

O esboço do gráfico de |ƒ(x − 3)| + 2 está representado na alternativa
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.





NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
Na circunferência de raio 1, representada na figura a seguir, os pontos M e N são tais que o arco de extremidades A e M mede π/2 rad e o arco de extremidades A e N mede - π/3 rad .

A distância entre os pontos M e N é
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.

2 - √3 .

NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
Considere o quadrado ABCD da figura a
seguir, em que G é o ponto médio de  , F é o ponto médio de
, F é o ponto médio de  e
e 

A razão entre a área do quadrilátero EFGD
e a área do quadrado ABCD é
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
Sendo a e b números reais positivos quaisquer, considere as afirmações abaixo.
I - Se a > b então ax >bx , para qualquer x ∈ R.
II - Se a > b >1, então
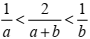 .
.
III- Se a > b , então √a > √b .
Quais estão corretas?
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
Desde a Grécia Antiga, sabe-se que a somados números ímpares consecutivos, a partir do 1, é sempre um quadrado perfeito. Como exemplo, tem-se
1 = 12
1 + 3 + 5 = 32
Então, a soma de todos os números ímpares menores do que 100 é
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
O valor numérico da expressão 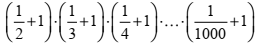 é
é
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
Considere as seguintes afirmações sobre quaisquer funções ƒ reais de variável real.
I - Se x ∈ R e x > 0, então ƒ(x) > 0 .
II - Se ƒ(x) = 0 , então x é zero da função ƒ(x).
III- Se x1 e x2 são números reais, com x1 < x2 , então ƒ( x1) < ƒ(x2) .
Quais estão corretas?
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
Considere a região delimitada pelas inequações x + y ≥ 1 e x2 + y2 ≤ 4 , representadas em um mesmo sistema de coordenadas cartesianas.
Assinale a alternativa que contém o gráfico que melhor representa essa região.





A representação geométrica das retas r e s encontra-se desenhada no sistema de coordenadas cartesianas na imagem a seguir.

Assinale a alternativa que apresenta o sistema
de equações lineares que pode representar as
retas r e s da imagem acima.





Considere o lugar geométrico dos pontos P =(x, y) que distam 3 unidades do ponto Q = (2, 3).
Assinale, entre as alternativas, o gráfico que pode representar esse lugar geométrico.





Uma partícula parte do ponto A e chega ao ponto H percorrendo a poligonal ABCDEFGH no cubo de aresta unitária, representado na figura abaixo.

A distância percorrida pela partícula é
No retângulo ABCD a seguir, estão marcados os pontos E, F e G de forma que o lado AB está dividido em 4 partes iguais e P é um ponto qualquer sobre o lado DC.

A razão entre a área do triângulo
PFG
e a
área do retângulo
ABCD
é