Questõesde UFPR sobre Matemática
Num teste de esforço físico, o movimento de um
indivíduo caminhando em uma esteira foi
registrado por um computador. A partir dos
dados coletados, foi gerado o gráfico da
distância percorrida, em metros, em função do
tempo, em minutos, mostrado ao lado:
De acordo com esse gráfico, considere as
seguintes afirmativas:
1. A velocidade média nos primeiros 4
minutos foi de 6 km/h.
2. Durante o teste, a esteira permaneceu
parada durante 2 minutos.
3. Durante o teste, a distância total percorrida
foi de 1200 m.
Assinale a alternativa correta.

Num teste de esforço físico, o movimento de um indivíduo caminhando em uma esteira foi registrado por um computador. A partir dos dados coletados, foi gerado o gráfico da distância percorrida, em metros, em função do tempo, em minutos, mostrado ao lado: De acordo com esse gráfico, considere as seguintes afirmativas:
1. A velocidade média nos primeiros 4 minutos foi de 6 km/h.
2. Durante o teste, a esteira permaneceu parada durante 2 minutos.
3. Durante o teste, a distância total percorrida foi de 1200 m.
Assinale a alternativa correta.

Sejam x,y ∈ (0,π/2), tais que cos(x)= 4/5 e sen(y)= 5/13. Podemos concluir que tg (x+y) é igual a:
Em quantos pontos do plano cartesiano a circunferência de equação (x - 2)2 + (y + 1 )2 = 9 e a parábola de equação y = -2x2 + 8x -6 se intersectam?
Em uma reunião de condomínio, os moradores resolveram fazer
um sorteio para decidir a ordem em que suas casas serão
pintadas. As 8 casas desse condomínio estão dispostas conforme
o esquema ao lado. Dizemos que duas casas são vizinhas quando
estão dispostas de frente ou de lado. Por exemplo, a casa 3 é
vizinha das casas 1, 4 e 5, enquanto a casa 8 é vizinha apenas das
casas 6 e 7.
Qual é a probabilidade das duas primeiras casas sorteadas serem
vizinhas?

Em uma reunião de condomínio, os moradores resolveram fazer um sorteio para decidir a ordem em que suas casas serão pintadas. As 8 casas desse condomínio estão dispostas conforme o esquema ao lado. Dizemos que duas casas são vizinhas quando estão dispostas de frente ou de lado. Por exemplo, a casa 3 é vizinha das casas 1, 4 e 5, enquanto a casa 8 é vizinha apenas das casas 6 e 7.
Qual é a probabilidade das duas primeiras casas sorteadas serem vizinhas?

Considere a seguinte sequência de funções polinomiais do segundo grau:

Denotando por S1 a soma das raízes de p1(x), S2 a soma das raízes de p2(x) e assim por diante, pode-se concluir que
a soma infinita
S = S1 + S2 + S3 + S4 + ...
é igual a:
Considere a seguinte sequência de funções polinomiais do segundo grau:

Denotando por S1 a soma das raízes de p1(x), S2 a soma das raízes de p2(x) e assim por diante, pode-se concluir que a soma infinita
S = S1 + S2 + S3 + S4 + ...
é igual a:
Um tanque contém uma solução de água e sal cuja concentração está diminuindo devido à adição de mais água.
Suponha que a concentração Q(t) de sal no tanque, em gramas por litro (g/l), decorridas t horas após o início da
diluição, seja dada por
Q(t) = 100 x 5 -0,3t
Assinale a alternativa que mais se aproxima do tempo necessário para que a concentração de sal diminua para 50 g/l.
(Use log5 = 0,7)
Um tanque contém uma solução de água e sal cuja concentração está diminuindo devido à adição de mais água. Suponha que a concentração Q(t) de sal no tanque, em gramas por litro (g/l), decorridas t horas após o início da diluição, seja dada por
Q(t) = 100 x 5 -0,3t
Assinale a alternativa que mais se aproxima do tempo necessário para que a concentração de sal diminua para 50 g/l.
(Use log5 = 0,7)
Giovana deseja fazer um painel usando folhas de papel de tamanhos carta e A4. O painel será composto por duas
faixas, cada uma contendo apenas folhas inteiras de um tipo dispostas lado a lado (sem sobreposição e sem espaço
entre elas), formando uma figura retangular, sem sobras e sem cortes de papel. As folhas do tipo carta (1) serão
dispostas na posição vertical, e as folhas do tipo A4 (2) serão dispostas na posição horizontal, conforme ilustra a figura
abaixo:

Sabendo que as folhas A4 têm tamanho 210 mm por 297 mm e que as folhas carta têm tamanho 216 mm por 279 mm,
a menor quantidade total de folhas de papel (incluindo A4 e carta) que Giovanna precisa usar para conseguir atender
às exigências do enunciado é:
Giovana deseja fazer um painel usando folhas de papel de tamanhos carta e A4. O painel será composto por duas faixas, cada uma contendo apenas folhas inteiras de um tipo dispostas lado a lado (sem sobreposição e sem espaço entre elas), formando uma figura retangular, sem sobras e sem cortes de papel. As folhas do tipo carta (1) serão dispostas na posição vertical, e as folhas do tipo A4 (2) serão dispostas na posição horizontal, conforme ilustra a figura abaixo:

Sabendo que as folhas A4 têm tamanho 210 mm por 297 mm e que as folhas carta têm tamanho 216 mm por 279 mm,
a menor quantidade total de folhas de papel (incluindo A4 e carta) que Giovanna precisa usar para conseguir atender
às exigências do enunciado é:
Diana pretende distribuir 6 litros de geleia em 25 potes iguais. Cada pote possui internamente o formato de um
paralelepípedo de base quadrada com 5 cm de lado. Dividindo igualmente a geleia em todos os potes, qual é a altura
interna que a geleia atingirá em cada recipiente?
Considere o conjunto S de todas as sequências de 5 letras formadas com as vogais A, E, I, O e U que satisfazem
simultaneamente às duas regras abaixo:
I. O número de letras A é igual ao número de letras E.
II. O número de letras O é igual ao número de letras U.
Por exemplo, as sequências UOIOU, AEIOU e IAEII satisfazem as duas regras acima, enquanto AAEEE não satisfaz a
primeira regra e IOIIO não satisfaz a segunda.
Quantos elementos distintos possui o conjunto S?
Considere o conjunto S de todas as sequências de 5 letras formadas com as vogais A, E, I, O e U que satisfazem simultaneamente às duas regras abaixo:
I. O número de letras A é igual ao número de letras E.
II. O número de letras O é igual ao número de letras U.
Por exemplo, as sequências UOIOU, AEIOU e IAEII satisfazem as duas regras acima, enquanto AAEEE não satisfaz a primeira regra e IOIIO não satisfaz a segunda.
Quantos elementos distintos possui o conjunto S?
Sobre as funções reais 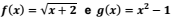 , identifique as afirmativas a seguir como verdadeiras (V) ou
falsas (F):
, identifique as afirmativas a seguir como verdadeiras (V) ou
falsas (F):
( ) O domínio da função ƒ é Dom(ƒ) = {x ∈ ℝ; x ≥ 0}.
( ) 
( ) A imagem de ƒ coincide com a imagem de g, ou seja, Im(ƒ) = Im(g).
( ) Os gráficos dessas funções se cruzam apenas uma vez.
Assinale a alternativa que apresenta a sequência correta, de cima para baixo.
Sobre as funções reais 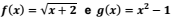 , identifique as afirmativas a seguir como verdadeiras (V) ou
falsas (F):
, identifique as afirmativas a seguir como verdadeiras (V) ou
falsas (F):
( ) O domínio da função ƒ é Dom(ƒ) = {x ∈ ℝ; x ≥ 0}.
( ) 
( ) A imagem de ƒ coincide com a imagem de g, ou seja, Im(ƒ) = Im(g).
( ) Os gráficos dessas funções se cruzam apenas uma vez.
Assinale a alternativa que apresenta a sequência correta, de cima para baixo.
A probabilidade de se vencer uma partida de certo jogo é de 10%. Quantas partidas devem ser jogadas em sequência
para que a probabilidade de que haja vitória em pelo menos uma delas seja superior a 99%? Se necessário, use
log(3) = 0,477.
A figura ao lado apresenta um molde para construção de uma pirâmide
hexagonal regular. Para montar essa pirâmide, basta recortar o molde
seguindo as linhas contínuas, dobrar corretamente nas linhas tracejadas
e montar a pirâmide usando as abas trapezoidais para fixar sua estrutura
com um pouco de cola. Sabendo que cada um dos triângulos tracejados
nesse molde é isósceles, com lados medindo 5 cm e 13 cm, qual das
alternativas abaixo mais se aproxima do volume dessa pirâmide?

