No triângulo equilátero ABC, H corresponde ao ponto médio do lado 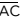 . Desse modo, a área
do triângulo ABH é igual à metade da área de ABC.
. Desse modo, a área
do triângulo ABH é igual à metade da área de ABC.

Sendo W o perímetro do triângulo ABH e Y o perímetro do triângulo ABC, uma relação correta
entre W e Y é:
No triângulo equilátero ABC, H corresponde ao ponto médio do lado 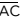 . Desse modo, a área
do triângulo ABH é igual à metade da área de ABC.
. Desse modo, a área
do triângulo ABH é igual à metade da área de ABC.

Sendo W o perímetro do triângulo ABH e Y o perímetro do triângulo ABC, uma relação correta
entre W e Y é:



















