O gráfico que pode representar a função dada por y = log3 x é
O gráfico que pode representar a função dada por y = log3 x é




O gráfico que pode representar a função dada por y = log3 x é




Júlia ficou sabendo, em sua aula de Ciências, que:
I. A concentração de antibiótico na corrente sangüínea de um animal decai exponencialmente e é dada por uma função da forma C(t) = C0at , em que C0 é a concentração de antibiótico no sangue do animal no instante em que é aplicado.
II. Uma colônia de bactérias cresce exponencialmente no corpo de um animal que não é submetido a um tratamento, e o número de bactérias em função do tempo t é dado pela função B(t) = B0bi , em que B0 é a quantidade inicial de bactérias no corpo do animal.
Com relação a essas duas situações, os valores de a e b são, necessariamente,
A figura abaixo representa um octaedro.

O número de vértices, V, de faces, F, e de arestas, A, são
O número de emissoras de rádio em funcionamento nas regiões do Brasil é o seguinte:
Região Sul(S) Sudeste(SE) Nordeste(NE) Norte(N)
Número de emissoras 300 400 200 100
O gráfico de colunas que representa corretamente esse número de emissoras por região é




No plano, o sistema 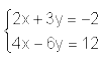 representa um par de retas
representa um par de retas


Foi feito um levantamento sobre o tempo fora da escola que os alunos dedicam aos estudos.
O resultado desse levantamento encontra-se no gráfico a seguir.

Mais de 45 alunos dedicam aos estudos fora da escola
Somente a desinfecção com cloro pode garantir água saudável e sem riscos para os banhistas. Para isso é recomendado o cloro granulado que deve ser misturado à água à razão de 15 g para cada 1 000 litros .
Para tratamento à base de cloro granulado em uma piscina retangular de 8 m por 15 m e profundidade de 1,20 m, serão necessários
Suponha que a mancha de crude continue aumentando nas águas do Golfo, na mesma proporção citada na reportagem.
A quantidade de litros de crude que representaria uma área equivalente ao território brasileiro, ou seja, de 8,5 milhões de km2 seria, aproximadamente, de
Leia o texto a seguir :
Uma catástrofe humanitária, econômica e ambiental.
“A plataforma petrolífera Deep Water Horizon afundou-se no final de Abril (22) passado e está na origem da maré negra cuja amplitude poucos ousam estimar. Desde o acidente que a BP multiplica-se em manobras técnicas para tentar controlar a fuga de crude do poço a mais de quilômetros e meio de profundidade.
(...) Neste momento ocupa uma área de quase 25 mil quilômetros quadrados, o equivalente à área geográfica da Sardenha, de acordo com um estudo da Universidade de Miami, nos Estados Unidos, o que representa uns 15 milhões de litros.”
(Fonte: http://pt.euronews.net em 22/06/2010).
Uma empresa de vendas contratou um engenheiro para a construção de um galpão num terreno retangular, de dimensões 12 m por 30 m . O galpão será dividido em 4 salas e um hall de entrada de 30 m2 , conforme mostra a figura abaixo:
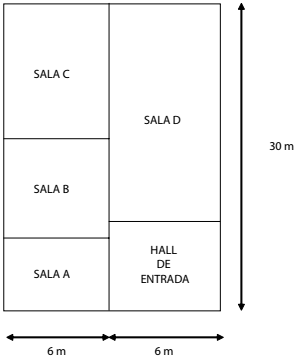
As áreas da salas A, B e C serão diretamente proporcionais aos números de funcionários que nela trabalharão . Na sala A, vão trabalhar 4 funcionários, na sala B, 5 funcionários e na sala C, 6 funcionários.
Sendo x, y e z as áreas das salas A, B e C, respectivamente, é CORRETO afirmar que
De acordo com o texto , em São Paulo , os números de celulares passarão a ter 10 dígitos, ao invés de 8 dígitos e todos começando com o código 10 ou 11. Porém, os números do tipo código de área + 90 não serão disponíveis aos moradores, pois são reservados para serviços de empresas .
Aprovada a proposta, a quantidade de novos números disponíveis para os assinantes de São Paulo, que iniciarão com código de área 10 e que, atualmente, começam por 6, 7, 8 ou 9 será equivalente a
“A Anatel divulgou esta semana que estuda aumentar o número de dígitos para celulares dos moradores do estado de São Paulo em mais dois dígitos.
O aumento no número de dígitos atingiria moradores da Cidade de São Paulo e da Região Metropolitana e aconteceria devido a dificuldade das operadores em encontrar combinações de números disponíveis para seus novos usuários.
Se a proposta for aprovada, a Anatel prevê o uso do DDD “11” (mesmo para chamadas locais) para todos os números já existentes. Já os novos números utilizariam um novo código de área (“10”).
Em resumo, caso aprovada, os usuários de São Paulo deverão inserir em suas ligações o código de área + o número do celular para efetuar ligações.”
(Fonte: Folha de São Paulo, 14 de maio 2010.)
Em um restaurante no centro da capital, foi observado o consumo das pessoas de duas mesas; tal consumo se fez da seguinte forma:
Número da mesa Quantidade de Quantidade de Valor total da
sanduíches sobremesas conta
01 2 3 R$ 23,40
02 6 4 R$ 55,20
Com base nos dados observados acima, pode-se afirmar CORRETAMENTE que uma pessoa,
ao consumir um sanduíche e uma sobremesa, pagará um total de
Joaquim, um jovem empreendedor, estuda duas possibilidades para investir R$10.000,00. A primeira opção é aplicar durante meio ano a uma taxa de juros simples de 0,5% a.m. e a segunda, aplicar o mesmo montante a uma taxa de juros compostos.
Assinale a alternativa que apresenta a taxa de juros compostos ao mês para que, com a mesma duração e com o mesmo montante inicial, Joaquim obtenha o mesmo rendimento da primeira possibilidade:
(Dados: 6√1,18 = 102797 * 10-5 ; 6√1,03 = 1004939 * 10-6 ;)