8a37a81d-c3
UEG 2018 - Matemática - Álgebra, Problemas
Uma concessionária vende um carro financiado em dois anos, e as parcelas mensais serão da seguinte maneira:
a primeira parcela será de R$ 1.000,00, e as demais decrescerão R$ 20,00 ao mês. Ao final do financiamento
esse carro terá custado ao comprador
Uma concessionária vende um carro financiado em dois anos, e as parcelas mensais serão da seguinte maneira:
a primeira parcela será de R$ 1.000,00, e as demais decrescerão R$ 20,00 ao mês. Ao final do financiamento
esse carro terá custado ao comprador
A
R$ 18.480,00
B
R$ 18.240,00
C
R$ 18.000,00
D
R$ 17.760,00
E
R$ 17.520,00






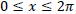 , para os quais as funções
, para os quais as funções 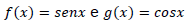 se interceptam, são
se interceptam, são