Questõesde UEFS sobre Matemática

InícioTodas as questões
1
1
Foram encontradas 147 questões
cf15931c-dc
UEFS 2010 - Matemática - Álgebra, Problemas

Uma fábrica produz dois tipos de equipamento X e Y, que lhe rendem, por unidade produzida, um lucro de R$300,00 e R$500,00, respectivamente.

Por motivos técnicos, em um determinado período, a capacidade de produção desses equipamentos é reduzida a, no máximo, 110 unidades de X e 86 unidades de Y, desde que o total não exceda a 150 unidades.

Nessas condições, o lucro máximo total que pode ser obtido nesse período, com a produção de X e Y é, em milhares de reais, igual a

A
53,0
B
62,2
C
76,0
D
86,5
E
110,0
cf10ebf9-dc
UEFS 2010 - Matemática - Números Complexos

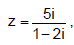Sendo considere o número complexo w com módulo igual ao de z e argumento principal medindo o dobro do argumento principal de z. Nessas condições, w pode ser representado algebricamente por

A

B

C

D

E

cf0b3f23-dc
UEFS 2010 - Matemática - Aritmética e Problemas, Porcentagem

Para quitar um débito de R$1 800,00 um devedor fez com o órgão credor um acordo de parcelamento da dívida nos seguintes termos:

• Prestações mensais fixas no valor de R$600,00, sendo a primeira paga imediatamente e admitindo-se a possibilidade da última prestação ser menor.

• Após o pagamento da primeira prestação, e antes do pagamento de cada parcela subsequente, a cada mês, serão acrescidos ao saldo devedor juros de 2%.

Nessas condições, após quitar a dívida, o valor total dos juros pagos foi aproximadamente igual a

A
R$36,00
B
R$36,40
C
R$37,21
D
R$37,50
E
R$38,00
cf026236-dc
UEFS 2010 - Matemática - Aritmética e Problemas, Regra de Três

Dois automóveis fizeram o mesmo percurso da cidade X até a cidade Z, passando pela cidade Y. O primeiro automóvel partiu de X, às 8 horas, e passou por Y, às 10h 20min, enquanto o segundo automóvel partiu de X, às 8h 30min, e passou por Y, às 10h 15min. Sabendo-se que os dois automóveis fizeram todo o percurso sem parar, mantendo suas velocidades constantes, e que o automóvel mais veloz chegou a Z, às 11h 30min, conclui-se que o outro, completou o percurso às

A
11h 45min.
B
12h.
C
12h 10min.
D
12h 25min.
E
13h.
cefdf921-dc
UEFS 2010 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas

Em uma cafeteria, o mesmo tipo de café é servido a um grupo de clientes, de acordo com as seguintes solicitações:

• M pediu 40ml de café adoçado com 2g de açúcar;
• N pediu 75ml de café adoçado com 3g de açúcar;
• P pediu 100ml de café adoçado com 6g de açúcar;
• Q pediu 150ml de café adoçado com 8g de açúcar.

Com base nas solicitações, pode-se afirmar que a concentração de açúcar no café pedido por

A
M é menor do que no de N.
B
M é maior do que no de P.
C
N é maior do que no de Q.
D
P é maior do que no de Q.
E
Q é menor do que no de N.
fdace4bd-b4
UEFS 2010 - Matemática - Circunferências e Círculos, Geometria Plana

Considerando-se as curvas C1: x2 + y2 = 16 e C2: x2 + y2 = 64 em um mesmo sistema de coordenadas cartesianas, é correto afirmar que uma circunferência tangente comum a essas curvas pode ter raio r e centro C tais que

A
r ∈ { 2, 6) e C ∈ { (x, y) / x2 + 2 = 4 }
B
r ∈ { 2, 6) e C ∈ { (x, y) / x2 + y2 = 36 }
C
r = 2 e C ∈ { (x, y)/ x2 + y2 = 4 }
D
r = 2 e C ∈ { (x, y)/ x2 + y2 = 36 } ou r = 6 e C ∈ { (x, y)/ x2 + y2 = 4 }
E
r = 2 e C ∈ { (x, y)/ x2 + y2 = 4 } ou r = 6 e C ∈ { (x, y) / x2 + y2 = 36 }
fda859d5-b4
UEFS 2010 - Matemática - Pontos e Retas, Geometria Analítica

Os pontos O = (0, 0), M = (√3, 1), N e P = (0, p) são vértices consecutivos de um losango. Sabendo-se que p > 0, pode-se concluir que o produto das coordenadas do ponto N é igual a

A
3 +√3
B
3√3
C
6
D
6 + 2√3
E
12
fda2b941-b4
UEFS 2010 - Matemática - Cone, Geometria Espacial

Um tronco de cone reto T tem altura h, raio da base menor r e raio da base maior R. Retirando-se de T um cone reto de altura h e base coincidente com a base menor do tronco, obtém-se um sólido cujo volume é igual ao volume do sólido retirado. Nessas condições, pode-se afirmar que

A
Rr + r2 − R2 = 0
B
Rr − r2 + R2 = 0
C
2Rr − r2 + R2 = 0
D
Rr − 2r2 + 2R2 = 0
E
2R2 − Rr − 2r2 = 0
fd9d1ebf-b4
UEFS 2010 - Matemática - Áreas e Perímetros, Geometria Plana

As retas r e s, na figura, são paralelas e o ponto P, vértice do ângulo reto do triângulo PRS, está a 3√3 unidades de distância da reta r e a 4 unidades de distância da reta s.


Se a área do triângulo PRS mede 24u.a. então o seu perímetro mede, em unidades de comprimento,

A
6√3
B
18+3√3
C
24
D
18+√3
E
28
fd974112-b4
UEFS 2010 - Matemática - Seno, Cosseno e Tangente, Trigonometria

Em um parque de diversões, uma roda gigante de raio r = 10m, tendo 12 cadeiras igualmente espaçadas ao longo de seu perímetro, faz uma volta completa em 30 segundos. Além disso, o ponto mais baixo atingido ao longo do percurso circular está a 0,5m do solo. Certo dia, depois de todos os assentos estarem ocupados, o assento 1 se encontrava na posição indicada na figura, quando a roda começa a girar no sentido anti-horário.

Sendo a distância desse assento ao solo, t segundos após a roda ter começado a girar, dada pela expressão D(t) =M+N sen(αt), α > 0, é correto afirmar que M − N é igual a

A
cos(5α)
B
sen(5α)
C
cos(10α)
D
sen(10α)
E
cos(15α)
fd91dc0f-b4
UEFS 2010 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas, Funções, Logaritmos, Frações e Números Decimais

Um recipiente com capacidade para 15 litros está completamente cheio de leite puro. Uma pessoa retira 3 litros desse leite e completa o recipiente com 3 litros de água. Em seguida, retira 3 litros dessa mistura leite/água e novamente completa o recipiente com 3 litros de água, repetindo esse processo sucessivas vezes.
Sendo k a fração da mistura final que corresponde ao leite e considerando-se, se necessário, log 2 = 0,3, pode-se afirmar que o menor valor de n tal que k = < 1/5 é

A
4
B
5
C
6
D
7
E
8
fd862b83-b4
UEFS 2010 - Matemática - Funções, Função de 2º Grau


Sabendo-se que todas as raízes do polinômio f(x), representadas graficamente na figura, são reais e que g-1(x) é a função inversa de g(x) = 2x – 1, pode-se concluir que o resto da divisão de f(x) por g-1(x) é

A
- 3
B
0
C
6
D
8
E
16
fd8c67c5-b4
UEFS 2010 - Matemática - Potenciação, Álgebra, Radiciação, Funções, Logaritmos

Representar um número real x em notação científica significa escrevê-lo na forma x = p. 10q , em que |p|∈[1, 10[ e q é um número inteiro.

Considerando-se log2 = 0,3 e representando x = 2364 em notação científica, encontra-se o valor de p igual a

A



B

C
2,1
D

√10

E
4,2
fd7bf0d3-b4
UEFS 2010 - Matemática - Análise Combinatória em Matemática

Um grupo de oito jovens vai ao teatro e compra ingressos, de modo a ocupar toda uma fileira que tem exatamente oito poltronas. Dois desses jovens, X e Y, são namorados e fazem questão de sentarem juntos, ocupando as poltronas centrais ou as poltronas das extremidades da fileira.

Sendo T o número total de formas distintas de todos se acomodarem, o valor de √T/30 é

A
5
B
8
C
9
D
12
E
13
fd81b9ef-b4
UEFS 2010 - Matemática - Aritmética e Problemas, Porcentagem

A despesa mensal de uma empresa na produção de um bem é composta por uma parcela fixa e uma parcela variável, proporcional ao número de peças produzidas. Sabe-se que

• o custo unitário de produção dessas peças é de R$1,50;
• o preço unitário de venda das peças produzidas é de R$2,40;
• não há lucro nem prejuízo na produção de 800 unidades mensais.

Com base nessas informações e sabendo-se que a empresa investe mensalmente R$95 000,00, pode-se afirmar que a produção mensal mínima, para que o lucro mensal total nas vendas seja de, pelo menos, 8% do valor investido no mês, é de n peças, para n igual a

A
9074
B
9120
C
9245
D
9400
E
9502
fd7640b7-b4
UEFS 2010 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas

Um feirante utiliza uma balança de dois pratos para fazer as suas vendas, mas possui apenas quatro pesos P, Q, R e S, considerados em ordem crescente de quantidades inteiras de kg, Colocando-se um, dois, três ou os quatro pesos em um mesmo prato, pode-se equilibrar, no outro, em valores inteiros, de 1kg até, no máximo, 15kg de mercadoria.

Para equilibrar 20kg de certa mercadoria colocada em um prato da balança, o feirante colocou, no outro prato, 8kg de mercadoria que ele havia pesado anteriormente, juntamente com alguns de seus pesos.

Nessas condições, os pesos utilizados foram

A
Q e S.
B
R e S.
C
P, Q e S.
D
P, R e S.
E
Q, R e S.
fd72e610-b4
UEFS 2010 - Matemática - Álgebra, Equação do 2º Grau e Problemas do 2º Grau

Considere a equação 2x2 − kx + k = 0, k ∈ R − {0}.

Escolhendo-se o coeficiente k aleatoriamente, dentre os elementos do conjunto X = {−3, −1, 0, 1, 2, 4, 5, 7, 8}, a chance de a equação obtida ter raízes complexas é

A
0
B
1/3
C
5/9
D
2/3
E
7/9
fd6d6a52-b4
UEFS 2010 - Matemática - Polinômios

Sendo α, β e γ raízes da equação x3 +4x2 −6x+3=0, é verdade que tg[(1/α + 1/β + 1/y) π/3] é igual a

A
√3/3
B
1
C
0
D
-√3
E
-2√3
fd682042-b4
UEFS 2010 - Matemática - Funções, Função de 1º Grau

O conjunto-solução da inequação x4 - 1/ -x4 +2x³ + 3x² maior ou igual a 0 é

A
−∞, − 1]
B
] −1, 1[
C
[1, 3[
D
[3, +∞[
E
] −∞, 1] ∪ ]3, +∞[
fd5e974d-b4
UEFS 2010 - Matemática - Números Complexos

Considerando-se os números complexos z = cos 5π/3 + isen 5π/3 e w = cos π/6 + isen π/6, é correto afirmar que o menor valor inteiro positivo de n que torna um número real positivo é

A
4
B
5
C
6
D
7
E
8