Questõesde UEFS sobre Matemática
Um tanque tem 1000 litros de álcool. Retiram-se dele 200 litros que são substituídos por água.
Mistura-se bem e, em seguida, retiram-se 200 litros dessa mistura que são substituídos por
água, e assim sucessivamente.
Após quatro retiradas, a quantidade de litros de álcool que resta na mistura é igual,
aproximadamente, a
O logaritmo de certo número, em uma dada base, é 3. A terça parte desse logaritmo, a base
e o número formam, nessa ordem, uma progressão aritmética.
Assim sendo, a base do logaritmo é um número compreendido entre
Uma pessoa gastou R$900,00 na compra de uma bicicleta, de um aparelho de som e de uma
câmera digital. A bicicleta custou R$60,00 a menos que a câmera digital, e o preço do aparelho
de som correspondeu a 80% do preço da bicicleta.
Nessas condições, o preço da câmera digital, em relação ao do aparelho de som, correspondeu a
A área da região limitada pelas desigualdades |x| + |y| ≤ 2 e |x| + |y| ≥ 1, é, em u.a, igual a

O produto das coordenadas do ponto P, indicado na figura, é igual a

O produto das coordenadas do ponto P, indicado na figura, é igual a

Sabendo-se que esse gráfico representa uma função da forma 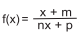 , para − 1 ≤ x ≤ 3,
pode-se afirmar corretamente que o valor de (n − m).p é
, para − 1 ≤ x ≤ 3,
pode-se afirmar corretamente que o valor de (n − m).p é

Sabendo-se que esse gráfico representa uma função da forma 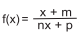 , para − 1 ≤ x ≤ 3,
pode-se afirmar corretamente que o valor de (n − m).p é
, para − 1 ≤ x ≤ 3,
pode-se afirmar corretamente que o valor de (n − m).p é
Seja a função f definida por f(x) = (2m + 1)x2 – 4x – 2m + 4,  .
.
Para que f admita raízes reais x1 e x2, com x1 < x2 < 1, o número real m deve ser tal que
 .
.






As pesquisas de um antropólogo revelaram que as populações indígenas de duas reservas,
A e B, variam de acordo com as funções f(t) = 2t + 2 + C1 e g(t) = 2t + 1 + C2, em que t é o tempo,
em anos, e as expressões f(t) e g(t) representam o número de indivíduos dessas reservas,
respectivamente. Os gráficos em evidência mostram o comportamento dessas funções.
Nessas condições, as duas reservas terão o mesmo número de indivíduos daqui a

As pesquisas de um antropólogo revelaram que as populações indígenas de duas reservas, A e B, variam de acordo com as funções f(t) = 2t + 2 + C1 e g(t) = 2t + 1 + C2, em que t é o tempo, em anos, e as expressões f(t) e g(t) representam o número de indivíduos dessas reservas, respectivamente. Os gráficos em evidência mostram o comportamento dessas funções.
Nessas condições, as duas reservas terão o mesmo número de indivíduos daqui a

O gráfico mostra o número de gols por temporada, marcados pelo atacante brasileiro Ronaldo
“fenômeno”, até maio de 2009.
Se não for considerado o ano de 2000, em que o craque esteve em tratamento de uma séria lesão
no joelho e praticamente não jogou, a sua média de gols entre 1997 e 2008 foi de, aproximadamente,

O gráfico mostra o número de gols por temporada, marcados pelo atacante brasileiro Ronaldo “fenômeno”, até maio de 2009.
Se não for considerado o ano de 2000, em que o craque esteve em tratamento de uma séria lesão
no joelho e praticamente não jogou, a sua média de gols entre 1997 e 2008 foi de, aproximadamente,
Considerando-se as curvas C1: x2 + y2 = 16 e C2: x2 + y2 = 64 em um mesmo sistema de
coordenadas cartesianas, é correto afirmar que uma circunferência tangente comum a essas
curvas pode ter raio r e centro C tais que
Um tronco de cone reto T tem altura h, raio da base menor r e raio da base maior R.
Retirando-se de T um cone reto de altura h e base coincidente com a base menor do tronco,
obtém-se um sólido cujo volume é igual ao volume do sólido retirado.
Nessas condições, pode-se afirmar que
Os pontos O = (0, 0), M = (√3, 1), N e P = (0, p) são vértices consecutivos de um losango.
Sabendo-se que p > 0, pode-se concluir que o produto das coordenadas do ponto N é igual a
As retas r e s, na figura, são paralelas e o ponto P, vértice do
ângulo reto do triângulo PRS, está a 3√3 unidades de distância
da reta r e a 4 unidades de distância da reta s.
Se a área do triângulo PRS mede 24u.a. então o seu perímetro
mede, em unidades de comprimento,


Em um parque de diversões, uma roda gigante de raio r = 10m, tendo
12 cadeiras igualmente espaçadas ao longo de seu perímetro, faz uma
volta completa em 30 segundos. Além disso, o ponto mais baixo atingido
ao longo do percurso circular está a 0,5m do solo. Certo dia, depois de
todos os assentos estarem ocupados, o assento 1 se encontrava na
posição indicada na figura, quando a roda começa a girar no sentido
anti-horário.
Sendo a distância desse assento ao solo, t segundos após a roda ter
começado a girar, dada pela expressão D(t) =M+N sen(αt), α > 0, é correto
afirmar que M − N é igual a


Um recipiente com capacidade para 15 litros está completamente cheio de leite puro. Uma
pessoa retira 3 litros desse leite e completa o recipiente com 3 litros de água. Em seguida,
retira 3 litros dessa mistura leite/água e novamente completa o recipiente com 3 litros de água,
repetindo esse processo sucessivas vezes.
Sendo k a fração da mistura final que corresponde ao leite e considerando-se, se necessário,
log 2 = 0,3, pode-se afirmar que o menor valor de n tal que k < 1/5 é
Representar um número real x em notação científica significa escrevê-lo na forma x = p. 10q
, em
que |p|∈[1, 10[ e q é um número inteiro.
Considerando-se log2 = 0,3 e representando x = 2364 em notação científica, encontra-se o valor
de p igual a


Sabendo-se que todas as raízes do polinômio f(x),
representadas graficamente na figura, são reais e que g-1(x)
é a função inversa de g(x) = 2x – 1, pode-se concluir que
o resto da divisão de f(x) por g-1(x) é

Sabendo-se que todas as raízes do polinômio f(x), representadas graficamente na figura, são reais e que g-1(x) é a função inversa de g(x) = 2x – 1, pode-se concluir que o resto da divisão de f(x) por g-1(x) é
