Questõesde UEFS sobre Matemática
Representar um número real x em notação científica significa escrevê-lo na forma x = p. 10q
, em
que |p|∈[1, 10[ e q é um número inteiro.
Considerando-se log2 = 0,3 e representando x = 2364 em notação científica, encontra-se o valor
de p igual a


Um grupo de oito jovens vai ao teatro e compra ingressos, de modo a ocupar toda uma fileira
que tem exatamente oito poltronas. Dois desses jovens, X e Y, são namorados e fazem questão
de sentarem juntos, ocupando as poltronas centrais ou as poltronas das extremidades da fileira.
Sendo T o número total de formas distintas de todos se acomodarem, o valor de 

A despesa mensal de uma empresa na produção de um bem é composta por uma parcela
fixa e uma parcela variável, proporcional ao número de peças produzidas.
Sabe-se que
• o custo unitário de produção dessas peças é de R$1,50;
• o preço unitário de venda das peças produzidas é de R$2,40;
• não há lucro nem prejuízo na produção de 800 unidades mensais.
Com base nessas informações e sabendo-se que a empresa investe mensalmente R$95 000,00,
pode-se afirmar que a produção mensal mínima, para que o lucro mensal total nas vendas seja
de, pelo menos, 8% do valor investido no mês, é de n peças, para n igual a
Sabendo-se que todas as raízes do polinômio f(x),
representadas graficamente na figura, são reais e que g-1(x)
é a função inversa de g(x) = 2x – 1, pode-se concluir que
o resto da divisão de f(x) por g-1(x) é


Considere a equação 2x2 − kx + k = 0, k ∈ R − {0}.
Escolhendo-se o coeficiente k aleatoriamente, dentre os elementos do conjunto
X = {−3, −1, 0, 1, 2, 4, 5, 7, 8}, a chance de a equação obtida ter raízes complexas é
Os irmãos X e Y, aos 10 e 14 anos de idade, respectivamente, receberam uma herança de
R$160 000,00 que foi dividida entre eles, em duas partes aplicadas a uma taxa fixa de juros simples
de 10% ao ano. Sobre a aplicação de cada irmão, sabe-se que
• nenhum depósito ou saque poderá ser feito até que o mesmo complete 18 anos;
• o montante da aplicação de X, quando este completar 18 anos, será o mesmo da aplicação
de Y, quando este completar 18 anos.
Assim, é verdade que
O conjunto-solução da inequação 
O conjunto-solução da inequação 
Considerando-se os números complexos Z = cos 5π/3 +isen 5π/3 e W = cosπ/6 + isen π/6 , é correto afirmar
que o menor valor inteiro positivo de n que torna um número real positivo é
Sendo α, β e γ raízes da equação x³
+4x² −6x+3=0, é verdade que 
Sendo α, β e γ raízes da equação x³
+4x² −6x+3=0, é verdade que 
Se a soma dos n primeiros termos de uma progressão aritmética é dada pela  expressão então a soma do segundo com o décimo termo dessa progressão é
expressão então a soma do segundo com o décimo termo dessa progressão é
Se a soma dos n primeiros termos de uma progressão aritmética é dada pela  expressão então a soma do segundo com o décimo termo dessa progressão é
expressão então a soma do segundo com o décimo termo dessa progressão é
O algarismo que se deve colocar entre os algarismos do número 68, para que o número obtido
seja divisível por 4 e 6 simultaneamente, é um elemento do conjunto
O conjunto X = {4m + 5n;m,n∈Z+} contém todos os números inteiros positivos
Considerando-se um sólido cujos vértices são os pontos de intersecção das diagonais das faces
de um cubo, cujas arestas medem xcm, é correto afirmar que seu volume é proporcional ao
volume do cubo e a razão de proporcionalidade é igual a
Na figura, os segmentos OR e PQ são lados paralelos do quadrilátero
OPQR, e o vértice Q é o ponto em que a função f(x) = 2(−x2 + 4x) assume
seu maior valor

Sendo a área da região sombreada igual a 18u.a., pode-se afirmar que
uma equação cartesiana da reta r que contém o lado RQ do
quadrilátero é
Na figura, os segmentos OR e PQ são lados paralelos do quadrilátero OPQR, e o vértice Q é o ponto em que a função f(x) = 2(−x2 + 4x) assume seu maior valor

Sendo a área da região sombreada igual a 18u.a., pode-se afirmar que
uma equação cartesiana da reta r que contém o lado RQ do
quadrilátero é
Considere, no sistema de coordenadas cartesianas, uma circunferência que tangencia o eixo
das ordenadas em y = √112 e também tangencia a reta √7y-3x = 0.
Sabendo-se que nenhum ponto da circunferência tem coordenadas negativas, pode-se afirmar
que a distância do centro da circunferência à origem é, em u.c., aproximadamente, igual a
O quadrado e o círculo representados na figura têm centro no mesmo
ponto e, nessa figura, as regiões sombreadas têm área de mesma
medida.

Nessas condições, pode-se afirmar que


O triângulo QRN, na figura, foi obtido, girando-se o triângulo MNO em torno do ponto N.
Sabendo-se que 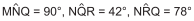 e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede
e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede

O triângulo QRN, na figura, foi obtido, girando-se o triângulo MNO em torno do ponto N.
Sabendo-se que 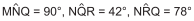 e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede
e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede

Estudos mostraram a viabilidade da construção de uma ponte ligando uma cidade litorânea a
uma ilha, a partir de um ponto P ou de um ponto Q da costa, distantes 2400m um do outro,
até um ponto I da referida ilha.
Sabe-se que se a ponte for construída a partir de P ou de Q, formará com PQ ângulos de 45º
e 60º, respectivamente, e que, nas duas situações, o custo de construção é de 100 unidades
monetárias por metro linear.
Com base nessas informações e considerando-se sen 75º = 0,96, √2=1,4 e √3=1,7, pode-se
afirmar que, optando-se pela construção da ponte menor, haverá uma economia, em unidades
monetárias, de

Estudos mostraram a viabilidade da construção de uma ponte ligando uma cidade litorânea a uma ilha, a partir de um ponto P ou de um ponto Q da costa, distantes 2400m um do outro, até um ponto I da referida ilha.
Sabe-se que se a ponte for construída a partir de P ou de Q, formará com PQ ângulos de 45º e 60º, respectivamente, e que, nas duas situações, o custo de construção é de 100 unidades monetárias por metro linear.
Com base nessas informações e considerando-se sen 75º = 0,96, √2=1,4 e √3=1,7, pode-se afirmar que, optando-se pela construção da ponte menor, haverá uma economia, em unidades monetárias, de
Se os arcos α, β e γ, nessa ordem, formam uma progressão aritmética, então a expressão
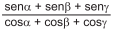 é equivalente a
é equivalente a
Se os arcos α, β e γ, nessa ordem, formam uma progressão aritmética, então a expressão
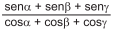 é equivalente a
é equivalente a