Questõesde UEFS sobre Matemática
Foram encontradas 175 questões
0c988ee6-e7
UEFS 2009 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas
O conjunto-imagem da função real f(x) = | – 3 + cos (2x)| + 1 é
O conjunto-imagem da função real f(x) = | – 3 + cos (2x)| + 1 é
A
[1, 2]
B
[2, 3]
C
[2, 4]
D
[3, 4]
E
[3, 5]
0c9d4f41-e7
UEFS 2009 - Matemática - Trigonometria, Círculo Trigonométrico
Sendo x um arco do 2o
quadrante, tal que senx = 1/3 , pode-se afirmar que o valor de A = √ 2 tgx é
igual ao valor de
Sendo x um arco do 2o
quadrante, tal que senx = 1/3 , pode-se afirmar que o valor de A = √ 2 tgx é
igual ao valor de
A
sen 2π/3
B
cos 2π/3
C
sen 5π/6
D
cos 5π/6
E
sen 4π/3
0c92157b-e7
UEFS 2009 - Matemática - Análise de Tabelas e Gráficos

Em um determinado concurso, 2000 candidatos inscritos compareceram às provas realizadas em um
grande colégio. O número de candidatos (y) que entraram no colégio, em função do horário de
entrada(t), é representado por pontos do gráfico, sendo t = 0 o instante em que os portões de acesso
foram abertos e t = 60, o instante em que esses portões foram fechados. Assim, pode-se afirmar que,
quando o número de candidatos no interior do colégio atingiu 1860, o tempo decorrido desde a
abertura dos portões foi igual a

Em um determinado concurso, 2000 candidatos inscritos compareceram às provas realizadas em um
grande colégio. O número de candidatos (y) que entraram no colégio, em função do horário de
entrada(t), é representado por pontos do gráfico, sendo t = 0 o instante em que os portões de acesso
foram abertos e t = 60, o instante em que esses portões foram fechados. Assim, pode-se afirmar que,
quando o número de candidatos no interior do colégio atingiu 1860, o tempo decorrido desde a
abertura dos portões foi igual a
A
53min20seg.
B
53min45seg.
C
54min 36seg.
D
55min20seg.
E
55min48seg.
0c8e60f5-e7
UEFS 2009 - Matemática - Álgebra Linear, Sistemas Lineares
Sendo 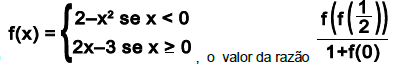 é igual a
é igual a
Sendo 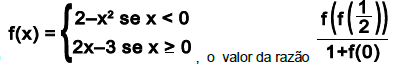 é igual a
é igual a
A
f(0)
B
f(1/2)
C
f(1)
D
f(2)
E
f(3/2)
0c8a129f-e7
UEFS 2009 - Matemática - Probabilidade
Ao se analisarem os resultados obtidos por uma turma de um determinado curso, levou-se em
consideração, dentre outros fatores, a frequência às aulas. Considerando-se uma amostra aleatória
de 10 alunos, constatou-se que o número total de faltas, no decorrer do curso, foi
0, 1, 2, 2, 2, 3, 4, 5, 5, 6.
Sorteando-se, ao acaso, um desses alunos, a probabilidade de o número de faltas ser maior do que
4, é igual a
Ao se analisarem os resultados obtidos por uma turma de um determinado curso, levou-se em
consideração, dentre outros fatores, a frequência às aulas. Considerando-se uma amostra aleatória
de 10 alunos, constatou-se que o número total de faltas, no decorrer do curso, foi
0, 1, 2, 2, 2, 3, 4, 5, 5, 6.
Sorteando-se, ao acaso, um desses alunos, a probabilidade de o número de faltas ser maior do que
4, é igual a
A
0,3
B
0,4
C
0,5
D
0,6
E
0,7
0c7ab3a5-e7
UEFS 2009 - Matemática - Álgebra, Problemas
Na divisão das despesas da família, cabe ao Sr. X pagar, mensalmente, R$850,00 do aluguel do
apartamento em que a família reside e, à Sra. X, pagar, mensalmente, R$400,00 relativos à taxa do
condomínio.
Sabendo-se que a renda mensal líquida do casal é igual a R$7820,00 e que, efetuando os
pagamentos citados, restará, à Sra. X, 4/5 do valor restante ao Sr. X, pode-se afirmar que a
diferença entre as rendas do Sr. e da Sra. X, em reais, está entre
Na divisão das despesas da família, cabe ao Sr. X pagar, mensalmente, R$850,00 do aluguel do
apartamento em que a família reside e, à Sra. X, pagar, mensalmente, R$400,00 relativos à taxa do
condomínio.
Sabendo-se que a renda mensal líquida do casal é igual a R$7820,00 e que, efetuando os
pagamentos citados, restará, à Sra. X, 4/5 do valor restante ao Sr. X, pode-se afirmar que a
diferença entre as rendas do Sr. e da Sra. X, em reais, está entre
A
700 e 800
B
800 e 900
C
900 e 1000
D
1000 e 1100
E
1100 e 1200
0c803a9a-e7
UEFS 2009 - Matemática - Polinômios
Desenvolvendo-se o binômio ( 5x - 2/x4)6 , obtém-se uma expressão algébrica cujo termo médio é
Desenvolvendo-se o binômio ( 5x - 2/x4)6 , obtém-se uma expressão algébrica cujo termo médio é
A
( -2 .104)/x9
B
( 2 .104)/x2
C
( -5 .103)/x4
D
(5.103)x5
E
104 x9
0c85be34-e7
UEFS 2009 - Matemática - Análise Combinatória em Matemática
O número de anagramas da palavra PROVA que não apresenta as duas vogais juntas é
O número de anagramas da palavra PROVA que não apresenta as duas vogais juntas é
A
24
B
36
C
48
D
60
E
72
0c74ef44-e7
UEFS 2009 - Matemática - Progressão Geométrica - PG, Progressões
Um polinômio P, de grau n, tem o coeficiente do termo de maior grau igual é a 1 e suas raízes
formam uma progressão geométrica de razão 3 cujo primeiro termo r1 = 3.
Sabendo-se que o termo independente de P igual a 315, pode-se concluir que o grau de P é igual a
Um polinômio P, de grau n, tem o coeficiente do termo de maior grau igual é a 1 e suas raízes
formam uma progressão geométrica de razão 3 cujo primeiro termo r1 = 3.
Sabendo-se que o termo independente de P igual a 315, pode-se concluir que o grau de P é igual a
A
3
B
5
C
7
D
8
E
10
0c715623-e7
UEFS 2009 - Matemática - Polinômios
A soma e o produto das raízes do polinômio P(x) = 2x²
+ bx + c são, respectivamente, – 6 e 5.
Assim, o valor mínimo que P(x) pode assumir pertence ao conjunto
A soma e o produto das raízes do polinômio P(x) = 2x²
+ bx + c são, respectivamente, – 6 e 5.
Assim, o valor mínimo que P(x) pode assumir pertence ao conjunto
A
{– 6 , – 4 , – 1}
B
{– 5, – 3, 0}
C
{– 8 ,1 , 6}
D
{2, 4, 5 }
E
{3, 7, 8 }
0c699edf-e7
UEFS 2009 - Matemática - Progressão Geométrica - PG, Progressões
A sequência (zn) é uma progressão geométrica cujo primeiro termo e razão são, respectivamente,
iguais a z1
= 1 – i e q = i.
Nessas condições, pode-se concluir que Z3/Z5 é igual a
A sequência (zn) é uma progressão geométrica cujo primeiro termo e razão são, respectivamente,
iguais a z1
= 1 – i e q = i.
Nessas condições, pode-se concluir que Z3/Z5 é igual a
A
-1
B
-i
C
1
D
i
E
1 + i
0c6e2d4f-e7
UEFS 2009 - Matemática - Circunferências e Círculos, Geometria Plana
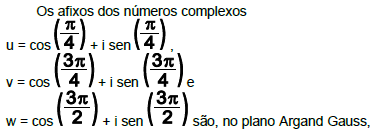
A
pontos colineares.
B
vértices de um triângulo equilátero.
C
vértices de um triângulo retângulo.
D
pontos de uma circunferência com centro na origem e raio 1.
E
pontos de uma circunferência com centro na origem e raio √ 2.
0c6686bd-e7
UEFS 2009 - Matemática - Aritmética e Problemas, Regra de Três
Duas pessoas fazem sua caminhada matinal em volta de uma praça partindo de um mesmo ponto,
no mesmo instante. Enquanto uma delas dá uma volta completa na praça em 9 minutos, a outra leva
6 minutos para completar uma volta.
Sabendo-se que o tempo da caminhada não deve exceder 1 hora e 20 minutos, pode-se concluir que
o número máximo de vezes que as duas pessoas podem voltar a se encontrar no ponto de partida,
nesse tempo, é igual a
Duas pessoas fazem sua caminhada matinal em volta de uma praça partindo de um mesmo ponto,
no mesmo instante. Enquanto uma delas dá uma volta completa na praça em 9 minutos, a outra leva
6 minutos para completar uma volta.
Sabendo-se que o tempo da caminhada não deve exceder 1 hora e 20 minutos, pode-se concluir que
o número máximo de vezes que as duas pessoas podem voltar a se encontrar no ponto de partida,
nesse tempo, é igual a
A
3
B
4
C
5
D
6
E
7
0c63824c-e7
UEFS 2009 - Matemática - Aritmética e Problemas, Porcentagem
Sobre um grupo de 40 analistas de sistema e programadores que atuam em uma grande empresa
de Informática, sabe-se que
· 80% dos programadores trabalham em tempo integral,
· 40% dos analistas trabalham em tempo parcial,
· apenas 5 programadores trabalham em tempo parcial.
Com base nesses dados, é possível afirmar que o total de
Sobre um grupo de 40 analistas de sistema e programadores que atuam em uma grande empresa
de Informática, sabe-se que
· 80% dos programadores trabalham em tempo integral,
· 40% dos analistas trabalham em tempo parcial,
· apenas 5 programadores trabalham em tempo parcial.
Com base nesses dados, é possível afirmar que o total de
A
analistas é igual a 12.
B
programadores é igual a 29.
C
15 programadores trabalham em tempo integral.
D
9 analistas trabalham em tempo integral.
E
13 pessoas desse grupo trabalham em tempo parcial.
e5b8eeda-e7
UEFS 2010 - Matemática - Pontos e Retas, Geometria Analítica
Os pontos O = (0, 0), M = (√3, 1) , N e P = (0, p) são vértices consecutivos de um losango.
Sabendo-se que p > 0, pode-se concluir que o produto das coordenadas do ponto N é igual a
Os pontos O = (0, 0), M = (√3, 1) , N e P = (0, p) são vértices consecutivos de um losango.
Sabendo-se que p > 0, pode-se concluir que o produto das coordenadas do ponto N é igual a
A
3 + √3
B
3√3
C
6
D
6 + 2√3
E
12
e5b5f49e-e7
UEFS 2010 - Matemática - Cone, Geometria Espacial
Um tronco de cone reto T tem altura h, raio da base menor r e raio da base maior R.
Retirando-se de T um cone reto de altura h e base coincidente com a base menor do tronco,
obtém-se um sólido cujo volume é igual ao volume do sólido retirado.
Nessas condições, pode-se afirmar que
Um tronco de cone reto T tem altura h, raio da base menor r e raio da base maior R.
Retirando-se de T um cone reto de altura h e base coincidente com a base menor do tronco,
obtém-se um sólido cujo volume é igual ao volume do sólido retirado.
Nessas condições, pode-se afirmar que
A
Rr + r² − R² = 0
B
Rr − r² + R² = 0
C
2Rr − r² + R² = 0
D
Rr − 2r² + 2R² = 0
E
2R² − Rr − 2r² = 0
e5bd29c6-e7
UEFS 2010 - Matemática - Circunferências e Círculos, Geometria Plana
Considerando-se as curvas C1: x² + y² = 16 e C2: x² + y² = 64 em um mesmo sistema de
coordenadas cartesianas, é correto afirmar que uma circunferência tangente comum a essas
curvas pode ter raio r e centro C tais que
Considerando-se as curvas C1: x² + y² = 16 e C2: x² + y² = 64 em um mesmo sistema de
coordenadas cartesianas, é correto afirmar que uma circunferência tangente comum a essas
curvas pode ter raio r e centro C tais que
A
r ∈ { 2, 6) e C ∈ { (x, y) / x² + y² = 4 }
B
r ∈ { 2, 6) e C ∈ { (x, y) / x² + y² = 36 }
C
r = 2 e C ∈ { (x, y)/ x²
+ y²
= 4 }
D
r = 2 e C ∈ { (x, y)/ x²
+ y²
= 36 } ou r = 6 e C ∈ { (x, y)/ x²
+ y²
= 4 }
E
r = 2 e C ∈ { (x, y)/ x²
+ y² = 4 } ou r = 6 e C ∈ { (x, y) / x²
+ y² = 36 }
e5afe6f3-e7
UEFS 2010 - Matemática - Circunferências e Círculos, Trigonometria, Geometria Plana, Funções Trigonométricas e Funções Trigonométricas Inversas
Em um parque de diversões, uma roda gigante de raio r = 10m, tendo
12 cadeiras igualmente espaçadas ao longo de seu perímetro, faz uma
volta completa em 30 segundos. Além disso, o ponto mais baixo atingido
ao longo do percurso circular está a 0,5m do solo. Certo dia, depois de
todos os assentos estarem ocupados, o assento 1 se encontrava na
posição indicada na figura, quando a roda começa a girar no sentido
anti-horário.

Sendo a distância desse assento ao solo, t segundos após a roda ter
começado a girar, dada pela expressão D(t) =M+N sen(αt), α > 0, é correto
afirmar que M − N é igual a
Em um parque de diversões, uma roda gigante de raio r = 10m, tendo
12 cadeiras igualmente espaçadas ao longo de seu perímetro, faz uma
volta completa em 30 segundos. Além disso, o ponto mais baixo atingido
ao longo do percurso circular está a 0,5m do solo. Certo dia, depois de
todos os assentos estarem ocupados, o assento 1 se encontrava na
posição indicada na figura, quando a roda começa a girar no sentido
anti-horário.

Sendo a distância desse assento ao solo, t segundos após a roda ter
começado a girar, dada pela expressão D(t) =M+N sen(αt), α > 0, é correto
afirmar que M − N é igual a
A
cos(5α)
B
sen(5α)
C
cos(10α)
D
sen(10α)
E
cos(15α)
e5b2eb3a-e7
UEFS 2010 - Matemática - Áreas e Perímetros, Geometria Plana
As retas r e s, na figura, são paralelas e o ponto P, vértice do
ângulo reto do triângulo PRS, está a 3√3 unidades de distância
da reta r e a 4 unidades de distância da reta s.

Se a área do triângulo PRS mede 24u.a. então o seu perímetro
mede, em unidades de comprimento
As retas r e s, na figura, são paralelas e o ponto P, vértice do
ângulo reto do triângulo PRS, está a 3√3 unidades de distância
da reta r e a 4 unidades de distância da reta s.

Se a área do triângulo PRS mede 24u.a. então o seu perímetro
mede, em unidades de comprimento
A
6√3
B
18 + 3√3
C
24
D
18 + √3
E
28