Na figura ao lado, ABCD é um quadrado de lado a. A
circunferência de raio x tangencia os lados AB e AD e a
semicircunferência de diâmetro CD.

O valor de x em função de a é
Na figura ao lado, ABCD é um quadrado de lado a. A circunferência de raio x tangencia os lados AB e AD e a semicircunferência de diâmetro CD.

O valor de x em função de a é






 .
.







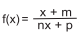 , para − 1 ≤ x ≤ 3,
pode-se afirmar corretamente que o valor de (n − m).p é
, para − 1 ≤ x ≤ 3,
pode-se afirmar corretamente que o valor de (n − m).p é



 = 90º,
= 90º,  = 42º,
= 42º,  = 78º e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo
= 78º e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo  mede
mede