
O triângulo QRN, na figura, foi obtido, girando-se o triângulo MNO em torno do ponto N.
Sabendo-se que 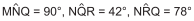 e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede
e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede

O triângulo QRN, na figura, foi obtido, girando-se o triângulo MNO em torno do ponto N.
Sabendo-se que 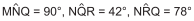 e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede
e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede
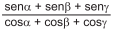 é equivalente a
é equivalente a

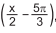 , é correto afirmar
que o conjunto-imagem e o período de f(x) são, respectivamente,
, é correto afirmar
que o conjunto-imagem e o período de f(x) são, respectivamente,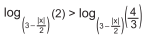 é um subconjunto de
é um subconjunto de


 é, aproximadamente,
é, aproximadamente,
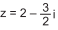 e QR, um arco medindo
e QR, um arco medindo 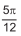 u.c.,
pode-se afirmar que o ponto R é afixo do número complexo que
pode ser representado, algebricamente, por
u.c.,
pode-se afirmar que o ponto R é afixo do número complexo que
pode ser representado, algebricamente, por





