cf34f362-dc
UEFS 2010 - Matemática - Funções, Função de 1º Grau

O gráfico representa a função real f(x) = acos(bx), em que a e b são constantes não nulas.
Sendo P= 5π /2 o período de f, o valor de 

O gráfico representa a função real f(x) = acos(bx), em que a e b são constantes não nulas.
Sendo P= 5π /2 o período de f, o valor de 

A
1/8
B
1/7
C
1/5
D
1/3
E
0


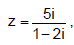 considere o número complexo w com módulo igual ao de z e argumento
principal medindo o dobro do argumento principal de z.
Nessas condições, w pode ser representado algebricamente por
considere o número complexo w com módulo igual ao de z e argumento
principal medindo o dobro do argumento principal de z.
Nessas condições, w pode ser representado algebricamente por







