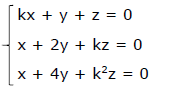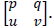5b8b6344-ff
UECE 2019 - Matemática - Polígonos, Geometria Plana
A medida, em metros, do lado de um
quadrado onde o comprimento de cada uma das
diagonais é 2 m é igual a
A medida, em metros, do lado de um
quadrado onde o comprimento de cada uma das
diagonais é 2 m é igual a
A
2√2.
B
√2.
C
√2/2 .
D
3√2.
 estão, nessa ordem,
em progressão aritmética é
estão, nessa ordem,
em progressão aritmética é 
 os números reais x
os números reais x